
ЁОЬтФПЁПГЄЩГЪаНЬг§ОжзщжЏВПЗжНЬЪІЗжБ№ЕНAЁЂBЁЂCЁЂDЫФИіЕиЗННјааПЮГЬХрбЕЃЌНЬг§ОжАДЖЈЖюЙКТђСЫЧАЭљЫФЕиЕФГЕЦБЃЌШчЭМ1ЪЧЮДжЦзїЭъГЩЕФГЕЦБжжРрКЭЪ§СПЕФЬѕаЮЭГМЦЭМЃЌЧыИљОнЭГМЦЭМЛиД№ЯТСаЮЪЬтЃК
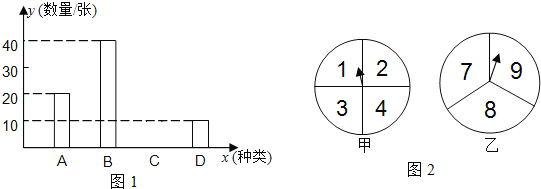
ЃЈ1ЃЉШєШЅAЕиЕФГЕЦБеМШЋВПГЕЦБЕФ20%ЃЌЧѓШЅCЕиЕФГЕЦБЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЈЭМ1ЃЉЃЛ
ЃЈ2ЃЉЧыДгаЁЕНДѓаДГіетЫФРрГЕЦБЪ§ЕФЪ§зжЃЌВЂжБНгаДГіетЫФИіЪ§ОнЕФЦНОљЪ§КЭжаЮЛЪ§ЃЛ
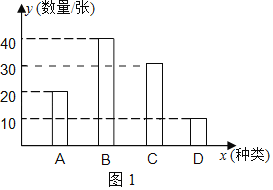
ЃЈ3ЃЉШчЭМ2ЃЌМззЊХЬБЛЗжГЩЫФЕШЗнЧвБъгаЪ§зж1ЁЂ2ЁЂ3ЁЂ4ЃЌввзЊХЬЗжГЩШ§ЕШЗнЧвБъгаЪ§зж7ЁЂ8ЁЂ9ЃЌОпЬхЙцЖЈЪЧЃКЭЌЪБзЊЖЏСНИізЊХЬЃЌЕБжИеыжИЯђЕФСНИіЪ§зжжЎКЭЪЧХМЪ§ЪБЃЌРюРЯЪІГіШЅХрбЕЃЌЗёдђеХРЯЪІГіШЅХрбЕЃЈжИеыжИдкЯпЩЯжизЊЃЉЃЌЪдгУЁАСаБэЗЈЁБЛђЁАЪїзДЭМЁБЕФЗНЗЈЗжЮіетИіЙцЖЈЖдЫЋЗНЪЧЗёЙЋЦНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ30еХЃЌМћНтЮіЃЛЃЈ2ЃЉ10ЁЂ20ЁЂ30ЁЂ40ЃЌЦНОљЪ§ЮЊ25ЃЌжаЮЛЪ§ЮЊ25ЃЛЃЈ3ЃЉЙЋЦНЃЌМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЯШгЩШЅAЕиЕФГЕЦБеМШЋВПГЕЦБЕФ20%ЧѓГіГЕЦБзмЪ§ЃЌзмЪ§СПМѕШЅAЁЂBЁЂDЕФЪ§СПМДПЩЧѓЕУCЕФЪ§СПЃЌДгЖјВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉНЋЫФИіЪ§зжДгаЁЕНДѓХХСаЃЌИљОнЦНОљЪ§КЭжаЮЛЪ§ЕФИХФюЧѓНтПЩЕУЃЛ
ЃЈ3ЃЉИљОнЬтвтгУСаБэЗЈЗжБ№ЧѓГіЕБжИеыжИЯђЕФСНИіЪ§зжжЎКЭЪЧХМЪ§ЪБЕФИХТЪЃЌМДПЩЧѓГіетИіЙцЖЈЖдЫЋЗНЪЧЗёЙЋЦНЃЎ
НтЃКЃЈ1ЃЉЁпШЋВПГЕЦБЪ§ЮЊ20ЁТ20%ЃН100ЃЈеХЃЉЃЌ
ЁрШЅCЕиГЕЦБЪ§ЮЊ100ЉЃЈ20+40+10ЃЉЃН30ЃЈеХЃЉЃЌ
ВЙШЋЭМаЮШчЯТЃК
ЃЈ2ЃЉДгаЁЕНДѓаДГіетЫФРрГЕЦБЪ§ЕФЪ§зжЮЊЃК10ЁЂ20ЁЂ30ЁЂ40ЃЌ
дђетЫФИіЪ§ОнЕФЦНОљЪ§ЮЊ![]() ЃН25ЃЌжаЮЛЪ§ЮЊ
ЃН25ЃЌжаЮЛЪ§ЮЊ![]() ЃН25ЃЛ
ЃН25ЃЛ
ЃЈ3ЃЉИљОнЬтвтСаБэШчЯТЃК
вђЮЊСНИіЪ§зжжЎКЭЪЧХМЪ§ЪБЕФИХТЪЪЧ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрРюРЯЪІГіШЅХрбЕЕФИХТЪКЭеХРЯЪІГіШЅХрбЕЕФИХТЪЯрЕШЃЌОљЮЊ![]() ЃЌ
ЃЌ
ЙЪетИіЙцЖЈЖдЫЋЗНЪЧЙЋЦНЕФЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛПщГЄ5УзПэ4УзЕФЕиЬКЃЌЮЊСЫУРЙлЩшМЦСЫСНКсЁЂСНзнЕФХфЩЋЬѕЮЦЃЈЭМжавѕгАВПЗжЃЉЃЌвбжЊХфЩЋЬѕЮЦЕФПэЖШЯрЭЌЃЌЫљеМУцЛ§ЪЧећИіЕиЬКУцЛ§ЕФ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХфЩЋЬѕЮЦЕФПэЖШЃЛ
ЃЈ2ЃЉШчЙћЕиЬКХфЩЋЬѕЮЦВПЗжУПЦНЗНУздьМл200дЊЃЌЦфгрВПЗжУПЦНЗНУздьМл100дЊЃЌЧѓЕиЬКЕФзмдьМлЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() СНЕу,гы
СНЕу,гы![]() жсНЛгкЕу
жсНЛгкЕу![]() .Еу
.Еу![]() дкКЏЪ§ЭМЯѓЩЯЃЌ
дкКЏЪ§ЭМЯѓЩЯЃЌ![]() жсЃЌЧв
жсЃЌЧв![]() ЃЌжБЯп
ЃЌжБЯп![]() ЪЧХзЮяЯпЕФЖдГЦжсЃЌ
ЪЧХзЮяЯпЕФЖдГЦжсЃЌ![]() ЪЧХзЮяЯпЕФЖЅЕу.
ЪЧХзЮяЯпЕФЖЅЕу.
(1)Чѓ![]() ЕФжЕ;
ЕФжЕ;
(2)ШчЭМЂйЃЌСЌНг![]() ЃЌ ЯпЖЮ
ЃЌ ЯпЖЮ![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕуF'ЧЁКУдкЯпЖЮBEЩЯЃЌЧѓЕу
ЕФЖдГЦЕуF'ЧЁКУдкЯпЖЮBEЩЯЃЌЧѓЕу![]() ЕФзјБъ;
ЕФзјБъ;
(3)ШчЭМЂк,ЖЏЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЙ§Еу
ЩЯЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЗжБ№гы
жсЕФДЙЯпЗжБ№гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌгыХзЮяЯпНЛгкЕу
ЃЌгыХзЮяЯпНЛгкЕу![]() .ЪдЮЪ:жБЯп
.ЪдЮЪ:жБЯп![]() гвВрЕФХзЮяЯпЩЯЪЧЗёДцдкЕу
гвВрЕФХзЮяЯпЩЯЪЧЗёДцдкЕу![]() ,ЪЙЕУ
,ЪЙЕУ![]() гы
гы![]() ЕФУцЛ§ЯрЕШЃЌЧвЯпЖЮ
ЕФУцЛ§ЯрЕШЃЌЧвЯпЖЮ![]() ЕФГЄЖШзюаЁ?ШчЙћДцдкЃЌЧѓГіЕу
ЕФГЄЖШзюаЁ?ШчЙћДцдкЃЌЧѓГіЕу![]() ЕФзјБъ;ШчЙћВЛДцдкЃЌЫЕУїРэгЩ.
ЕФзјБъ;ШчЙћВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
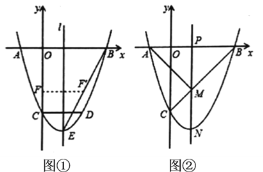
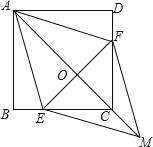
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуEЁЂFЗжБ№дкBCКЭCDЩЯЃЌAE=AFЃЎ
ЃЈ1ЃЉЧѓжЄЃКCE=CFЃЎ
ЃЈ2ЃЉСЌНгACНЛEFгкЕуOЃЌбгГЄOCжСЕуMЃЌЪЙOM=OAЃЌСЌНгEMЁЂFMЃЎХаЖЯЫФБпаЮAEMFЪЧЪВУДЬиЪтЫФБпаЮЃПВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
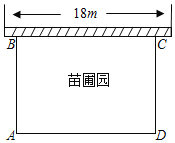
ЁОЬтФПЁПФГжабЇПЮЭтаЫШЄЛюЖЏаЁзщзМБИЮЇНЈвЛИіОиаЮЕФУчЦддВЃЎЦфжавЛБпППЧНЃЌСэЭтШ§БпгУГЄЮЊ40mЕФРщАЪЮЇГЩЃЎвбжЊЧНГЄЮЊ18mЃЈШчЭМЫљЪОЃЉЃЌЩшетИіУчЦддАДЙжБгкЧНЕФвЛБпABЮЊxm
ЃЈ1ЃЉгУКЌгаxЕФЪНзгБэЪОADЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєУчЦддАЕФУцЛ§ЮЊ192m2ЦНЗНУзЃЌЧѓABЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖрЖрАрГЄЭГМЦШЅФъ1ЁЋ8дТЁАЪщЯуаЃдАЁБЛюЖЏжаШЋАрЭЌбЇЕФПЮЭтдФЖСЪ§СПЃЈЕЅЮЛЃКБОЃЉЃЌЛцжЦСЫШчЭМелЯпЭГМЦЭМЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ

A.МЋВюЪЧ47B.жкЪ§ЪЧ42
C.жаЮЛЪ§ЪЧ58D.УПдТдФЖСЪ§СПГЌЙ§40ЕФга4ИідТ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєжабЇЩњЬхжЪНЁПЕзлКЯЦРЖЈГЩМЈЮЊxЗжЃЌТњЗжЮЊ100ЗжЃЎЙцЖЈЃК85ЁмxЁм100ЮЊAМЖЃЌ75ЁмxЃМ85ЮЊBМЖЃЌ60ЁмxЃМ75ЮЊCМЖЃЌxЃМ60ЮЊDМЖЃЎЯжЫцЛњГщШЁФГжабЇВПЗжбЇЩњЕФзлКЯЦРЖЈГЩМЈЃЌећРэЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
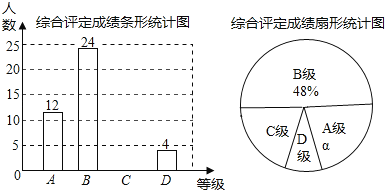
ЧыИљОнЭМжаЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкетДЮЕїВщжаЃЌвЛЙВГщШЁСЫЁЁ ЁЁУћбЇЩњЃЛaЃНЁЁ ЁЁ%ЃЛCМЖЖдгІЕФдВаФНЧЮЊЁЁ ЁЁЖШЃЎ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУаЃЙВга2000УћбЇЩњЃЌЧыФуЙРМЦИУаЃDМЖбЇЩњгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌдђЯТУцНсТлжаВЛе§ШЗЕФЪЧЃЈ ЃЉ
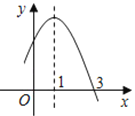
A.acЃМ0
B.2a+bЃН0
C.b2ЃМ4ac
D.ЗНГЬax2+bx+cЃН0ЕФИљЪЧЉ1ЃЌ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌдкЦНааЫФБпаЮABCDжаЃЌAB=20ЃЌ AD=30ЃЌЁЯABC=60Ёу ЃЌЕуPДгЕуDГіЗЂбиDCЯђЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊУПУы3ИіЕЅЮЛГЄЖШЃЛ ЭЌЪБЃЌЕуQДгЕуBГіЗЂбиBAЯђЕуAдШЫйдЫЖЏЃЌЫйЖШЮЊУПУы2ИіЕЅЮЛГЄЖШ.ЕБЕуPЭЃжЙдЫЖЏЪБЃЌЕуQвВЫцжЎЭЃжЙдЫЖЏ. Й§ЕуPзїPMЁЭADНЛADгкЕуM ЃЌСЌНгPQЃЌQM ЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЈ![]() ЃЉ.
ЃЉ.
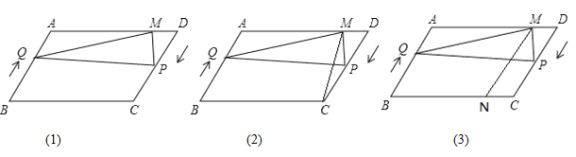
ЃЈ1ЃЉЕБQPЁЭPMЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉСЌНгMCЃЌЪЧЗёДцдкtжЕ ЃЌЪЙЕУЁїPQMЕФУцЛ§ЪЧЦНааЫФБпаЮABCDУцЛ§ЕФ![]() ЃП ШєДцдкЃЌЧѓГіЖдгІЕФtжЕЃЛШєВЛДцдкЃЌ ЧыЫЕУїРэгЩЃЛ
ЃП ШєДцдкЃЌЧѓГіЖдгІЕФtжЕЃЛШєВЛДцдкЃЌ ЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМЃЈ3ЃЉЃЌЙ§ЕуMзїMN//ABНЛгкЕуNЃЌЪЧЗё ДцдкtЕФжЕЃЌ ЪЙЕУЕуPдкЯпЖЮMNЕФДЙжБЦНЗжЯпЩЯЃП ШєДцдкЃЌ ЧѓГіЖдгІЕФtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com