
【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t小时,两车之间的距离为s千米,图中折线A-B-C-D表示s与t之间的函数关系.
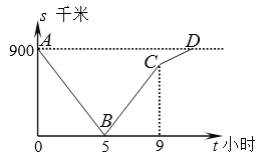
(1)求快车速度.
(2)当快车到达乙地时,慢车还要多少时间才能到达甲地.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
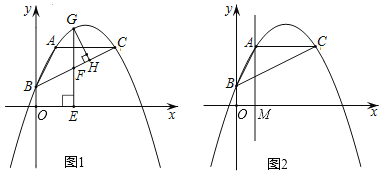
【题目】在平面直角坐标系中,抛物线y![]() bx+c,经过点A(1,3)、B(0,1),过点A作x轴的平行线交抛物线于另一点C
bx+c,经过点A(1,3)、B(0,1),过点A作x轴的平行线交抛物线于另一点C
(1)求抛物线的表达式及其顶点坐标;
(2)如图1,点G是BC上方抛物线上的一个动点,分别过点G作GH⊥BC于点H、作GE⊥x轴于点E,交BC于点F,在点G运动的过程中,△GFH的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图2,过A点的直线垂直x轴于点M,点N为直线AM上任意一点,当△BCN为直角三角形时,请直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市实验中学计划在暑假第二周的星期一至星期五开展暑假社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)乙同学随机选择两天,其中有一天是星期三的概率是多少?(列表或画树形图或列举)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“精准扶贫”是巩固温饱成果,加快脱贫致富步伐,实现中华民族伟大复兴“中国梦”的重要保障.某驻村帮扶小组因地制宜,积极筹集资金帮助所驻村建起了一个民族工艺品加工厂.现在,工厂计划加工1000件![]() 、
、![]() 两种工艺品,现有生产这两种工艺品所需的甲种材料445米,乙种材料510米,每生产1件
两种工艺品,现有生产这两种工艺品所需的甲种材料445米,乙种材料510米,每生产1件![]() 工艺品和1件
工艺品和1件![]() 工艺品所需甲、乙两种材料及生产成本、利润如下表:
工艺品所需甲、乙两种材料及生产成本、利润如下表:
甲材料(单位:米) | 乙材料(单位:米) | 生产成本(单位:元) | 利润(单位:元) | |
| 0.4 | 0.6 | 60 | 25 |
| 0.5 | 0.3 | 45 | 20 |
设生产![]() 种工艺品
种工艺品![]() 件,1000件
件,1000件![]() 、
、![]() 两种工艺品销售完的总利润为
两种工艺品销售完的总利润为![]() 元,根据上述信息,解答下列问题:
元,根据上述信息,解答下列问题:
(1)求![]() 与
与![]() 的函数解析式(也称关系式),并直接写出
的函数解析式(也称关系式),并直接写出![]() 的取值范围;
的取值范围;
(2)若要使加工成本不超过53400元,则有几种加工方案?那种方案的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,若有两条中线互相垂直,则称该三角形为中垂三角形.
(1)如图(1),![]() 是中垂三角形,
是中垂三角形,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的中线,且
边上的中线,且![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() 是等腰三角形.
是等腰三角形.
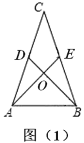


(2)如图(2),在中垂三角形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的中线,且
上的中线,且![]() 于点
于点![]() ,猜想
,猜想![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
(3)如图(3),四边形![]() 是菱形,对角线
是菱形,对角线![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 并延长,交于点
并延长,交于点![]() .
.
①求证:![]() 是中垂三角形;
是中垂三角形;
②若![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
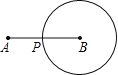
【题目】如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动
过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( )
A.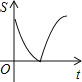 B.
B.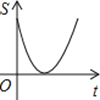 C.
C.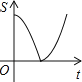 D.
D.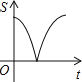
查看答案和解析>>
科目:初中数学 来源: 题型:
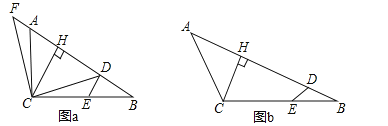
【题目】如图,在△ABC中,BC>AC,点E在BC上,CE=CA,点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图a,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F.
①求证:FA=DE;
②请猜想三条线段DE,AD,CH之间的数量关系,直接写出结论;
(2)如图b,当∠ACB=120°时,三条线段DE,AD,CH之间存在怎样的数量关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
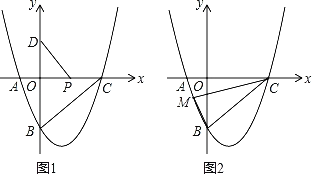
【题目】二次函数y=ax2﹣2x+c的图象与x轴交于A、C两点,点C(3,0),与y轴交于点B(0,﹣3).
(1)a= ,c= ;
(2)如图1,P是x轴上一动点,点D(0,1)在y轴上,连接PD,求![]() PD+PC的最小值;
PD+PC的最小值;
(3)如图2,点M在抛物线上,若S△MBC=3,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com