
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy![]() bx+cЃЌОЙ§ЕуAЃЈ1ЃЌ3ЃЉЁЂBЃЈ0ЃЌ1ЃЉЃЌЙ§ЕуAзїxжсЕФЦНааЯпНЛХзЮяЯпгкСэвЛЕуC
bx+cЃЌОЙ§ЕуAЃЈ1ЃЌ3ЃЉЁЂBЃЈ0ЃЌ1ЃЉЃЌЙ§ЕуAзїxжсЕФЦНааЯпНЛХзЮяЯпгкСэвЛЕуC
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНМАЦфЖЅЕузјБъЃЛ
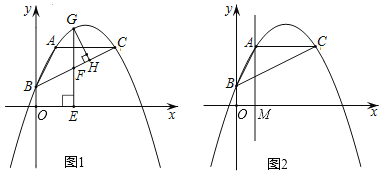
ЃЈ2ЃЉШчЭМ1ЃЌЕуGЪЧBCЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЗжБ№Й§ЕуGзїGHЁЭBCгкЕуHЁЂзїGEЁЭxжсгкЕуEЃЌНЛBCгкЕуFЃЌдкЕуGдЫЖЏЕФЙ§ГЬжаЃЌЁїGFHЕФжмГЄЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіетИізюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§AЕуЕФжБЯпДЙжБxжсгкЕуMЃЌЕуNЮЊжБЯпAMЩЯШЮвтвЛЕуЃЌЕБЁїBCNЮЊжБНЧШ§НЧаЮЪБЃЌЧыжБНгаДГіЕуNЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ,
,![]() ЃЛЃЈ2ЃЉМћНтЮі;ЃЈ3ЃЉЃЈ1ЃЌ0ЃЉЛђЃЈ1ЃЌ4ЃЉЛђЃЈ1ЃЌЉ1ЃЉЛђЃЈ1ЃЌ9ЃЉ.
ЃЛЃЈ2ЃЉМћНтЮі;ЃЈ3ЃЉЃЈ1ЃЌ0ЃЉЛђЃЈ1ЃЌ4ЃЉЛђЃЈ1ЃЌЉ1ЃЉЛђЃЈ1ЃЌ9ЃЉ.
ЁОНтЮіЁП
ЃЈ1ЃЉжагЩД§ЖЈЯЕЪ§ЗЈМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЯШгЩЬтвтЧѓГіЕуCЃЈ4ЃЌ3ЃЉЃЌЕУГіжБЯпBCЕФЗНГЬЮЊy=![]() x+1ЃЌЧѓГіBC=2
x+1ЃЌЧѓГіBC=2![]() ЃЌгжИљОнЁїBCIЁзЁїFGHЕУГіЁЯBCI=ЁЯFGHЃЌДгЖјtanЁЯBCI=tanЁЯFGH=
ЃЌгжИљОнЁїBCIЁзЁїFGHЕУГіЁЯBCI=ЁЯFGHЃЌДгЖјtanЁЯBCI=tanЁЯFGH=![]() ЃЌG(xЃЌ
ЃЌG(xЃЌ![]() x2+
x2+![]() x+1)ЃЌдђF(xЃЌ
x+1)ЃЌдђF(xЃЌ![]() x+1)ЕУГіGF=
x+1)ЕУГіGF=![]() (x2)2+2ЃЌЫљвдПЩЕУЕБx=2ЪБЃЌGFзюГЄЃЌДЫЪБЁїGFHжмГЄзюДѓЃЎгЩЯрЫЦБШМАе§ЧаКЏЪ§ЕФаджЪМДПЩЧѓЕУЁїGFHЕФжмГЄЮЊЃКGF+FH+GH=2+
(x2)2+2ЃЌЫљвдПЩЕУЕБx=2ЪБЃЌGFзюГЄЃЌДЫЪБЁїGFHжмГЄзюДѓЃЎгЩЯрЫЦБШМАе§ЧаКЏЪ§ЕФаджЪМДПЩЧѓЕУЁїGFHЕФжмГЄЮЊЃКGF+FH+GH=2+![]() +2ЃЛ
+2ЃЛ
ЃЈ3ЃЉЩшNЃЈ1ЃЌnЃЉгЩвбжЊBЃЈ0ЃЌ1ЃЉЃЌCЃЈ4ЃЌ3ЃЉПЩЧѓГіBN2=12+ЃЈn-1ЃЉ2=n2-2n+2ЃЌCN2=32+ЃЈn-3ЃЉ2=n2-6n+18ЃЌBC2=42+22=20ЃЌЗжШ§жжадПіЬжТлЃКЕБЁЯBNC=90ЁуЪБЃЌBN2+CN2=BC2ЃЌЕУn1=0ЃЌn2=4ЃЛЕБЁЯCBN=90ЁуЪБЃЌBN2+BC2=CN2ЃЌЕУn3=-1ЕБЁЯBCN=90ЁуЪБЃЌBC2+CN2=BN2ЃЌЕУn4=9зюКѓЕУNЕуЕФзјБъЮЊЃКЃЈ1ЃЌ0ЃЉЛђЃЈ1ЃЌ4ЃЉЛђЃЈ1ЃЌ-1ЃЉЛђЃЈ1ЃЌ9ЃЉЃЎ
ЃЈ1ЃЉЁпХзЮяЯпy![]() bx+cЃЌОЙ§ЕуAЃЈ1ЃЌ3ЃЉЁЂBЃЈ0ЃЌ1ЃЉЃЌ
bx+cЃЌОЙ§ЕуAЃЈ1ЃЌ3ЃЉЁЂBЃЈ0ЃЌ1ЃЉЃЌ
Ёр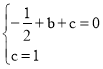 НтЕУЃК
НтЕУЃК![]() ЃЌc=1
ЃЌc=1
ЁрХзЮяЯпЕФБэДяЪНЮЊЃК![]()
Ёп![]() ЃЌ
ЃЌ![]()
ЁрЖЅЕузјБъЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпAЃЈ1ЃЌ3ЃЉЃЌЁрАбy=3ДњШы![]() ЃЌПЩЕУx1=1ЃЌxЃЌ2=4
ЃЌПЩЕУx1=1ЃЌxЃЌ2=4
ЁрCЃЈ4ЃЌ3ЃЉ
гЩBЃЈ0ЃЌ1ЃЉЁЂCЃЈ4ЃЌ3ЃЉ
ЕУжБЯпBCЕФБэДяЪНЮЊ![]() ЃЌBC
ЃЌBC![]()
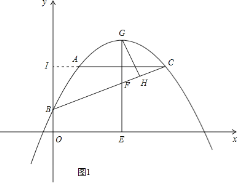
бгГЄCAгыyжсНЛгкЕуIЃЌдђIЃЈ0ЃЌ3ЃЉ
ЁпЕуGЪЧBCЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЗжБ№Й§ЕуGзїGHЁЭBCгкЕуHЁЂзїGEЁЭxжсгкЕуEЃЌНЛBCгкЕуFЃЌ
ЁрЁїBCIЁзЁїFGH
ЁрЁЯBCI=ЁЯFGH
ЁпtanЁЯBCI![]() ЃЌ
ЃЌ
ЁрtanЁЯFGH![]()
Щш![]() ЃЌдђ
ЃЌдђ![]()
ЁрGF![]()
ЁрЕБx=2ЪБЃЌGFзюГЄЃЌДЫЪБЁїGFHжмГЄзюДѓЃЎ
ЁрGF=2
Ёп![]()
Ёр![]()
ЁрGH![]()
ЁїGFHЕФжмГЄЮЊЃКGF+FH+GH=2![]() 2ЃЛ
2ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌгЩЬтвтЃЌЩшNЃЈ1ЃЌnЃЉ
ЁпBЃЈ0ЃЌ1ЃЉЁЂCЃЈ4ЃЌ3ЃЉ
ЁрBN2=12+ЃЈnЉ1ЃЉ2=n2Љ2n+2ЃЌ
CN2=32+ЃЈnЉ3ЃЉ2=n2Љ6n+18ЃЌ
BC2=42+22=20
ЕБЁЯBNC=90ЁуЪБЃЌBN2+CN2=BC2ЃЌМДЃЈn2Љ2n+2ЃЉ+ЃЈn2Љ6n+18ЃЉ=20
ЕУn1=0ЃЌn2=4ЃЛ
ЕБЁЯCBN=90ЁуЪБЃЌBN2+BC2=CN2ЃЌМДЃЈn2Љ2n+2ЃЉ+20=n2Љ6n+18
ЕУn3=Љ1
ЕБЁЯBCN=90ЁуЪБЃЌBC2+CN2=BN2ЃЌМД20+n2Љ6n+18=n2Љ2n+2
ЕУn4=9
злЩЯЫљЪіЃКNЕуЕФзјБъЮЊЃКЃЈ1ЃЌ0ЃЉЛђЃЈ1ЃЌ4ЃЉЛђЃЈ1ЃЌЉ1ЃЉЛђЃЈ1ЃЌ9ЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁРюЭЌбЇИљОн6ЮЛЭЌбЇдквЛДЮЪ§бЇВтЪджаЕФГЩМЈЛцжЦСЫвЛЬѕаЮЭГМЦЭМ(ШчЭМ).
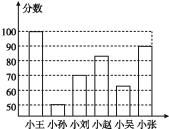
(1)ФФЮЛЭЌбЇЕФЗжЪ§зюИпЃЌФФЮЛЭЌбЇЕФЗжЪ§зюЕЭЃЌЫћУЧЯрВюЖрЩй?
(2)аЁеХЕФЗжЪ§ЪЧаЁЫяЗжЪ§ЕФМИБЖ?
(3)етИіЭМвзЪЙШЫВњЩњДэЮѓЕФИаОѕТ№?ЮЊЪВУД?
(4)ЮЊСЫИќЮЊжБЙлЁЂЧхГўЕиЗДгГет6УћЭЌбЇЕФЗжЪ§зДПі,етИіЭМгІзідѕбљЕФИФЖЏ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕкЪЎЖўНьаЃдАвеЪѕНке§дкШчЛ№ШчнБЕФНјааЃЌЮваЃОХФъМЖзщжЏ1500УћбЇЩњВЮМгСЫвЛДЮЁАЯцвЛЧщаЃдАжЊЪЖЁБДѓШќЃЎШќКѓЗЂЯжЫљгаВЮШќбЇЩњЕФГЩМЈОљВЛЕЭгк60ЗжЃЌЮЊСЫИќКУЕиСЫНтБОДЮДѓШќЕФГЩМЈЗжВМЧщПіЃЌЫцЛњГщШЁСЫЦфжаШєИЩУћбЇЩњЕФГЩМЈзїЮЊбљБОЃЌГЩМЈШчЯТЃК
90ЃЌ92ЃЌ81ЃЌ82ЃЌ78ЃЌ95ЃЌ86ЃЌ88ЃЌ72ЃЌ66ЃЌ62ЃЌ68ЃЌ89ЃЌ86ЃЌ93ЃЌ97ЃЌ100ЃЌ73ЃЌ76ЃЌ80ЃЌ77ЃЌ81ЃЌ86ЃЌ89ЃЌ82ЃЌ85ЃЌ71ЃЌ68ЃЌ74ЃЌ98ЃЌ90ЃЌ97ЃЌ100ЃЌ84ЃЌ87ЃЌ73ЃЌ65ЃЌ92ЃЌ96ЃЌ60ЃЎ
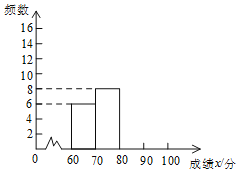
ЖдЩЯЪіГЩМЈНјааСЫећРэЃЌЕУЕНЯТСаВЛЭъећЕФЭГМЦЭМБэЃК
ГЩМЈx/Зж | ЦЕЪ§ | ЦЕТЪ |
60ЁмxЃМ70 | 6 | 0.15 |
70ЁмxЃМ80 | 8 | 0.2 |
80ЁмxЃМ90 | a | b |
90ЁмxЁм100 | c | d |
ЧыИљОнЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЌcЃНЁЁ ЁЁЃЌdЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШєГЩМЈдк90ЗжвдЩЯЃЈАќРЈ90ЗжЃЉЕФЮЊЁАгХЁБЕШЃЌЧыФуЙРМЦВЮМгетДЮБШШќЕФ1500УћбЇЩњжаГЩМЈЁАгХЁБЕШЕФдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТУцЫФИіУќЬтЃЌЦфжаецУќЬтЕФИіЪ§гаЃЈ ЃЉ
(1)ЦНЗжЯвЕФжБОЖДЙжБгкетЬѕЯвЃЌВЂЧвЦНЗжетЬѕЯвЫљЖдЕФЛЁЃЛ
(2)90ЁуЕФдВжмНЧЫљЖдЕФЯвЪЧжБОЖЃЛ
(3)дкЭЌдВЛђЕШдВжаЃЌдВаФНЧЕФЖШЪ§ЪЧдВжмНЧЕФЖШЪ§ЕФСНБЖЃЛ
(4)ШчЯТЭМЃЌЫГДЮСЌНгдВЕФШЮвтСНЬѕжБОЖЕФЖЫЕуЃЌЫљЕУЕФЫФБпаЮвЛЖЈЪЧОиаЮЃЎ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
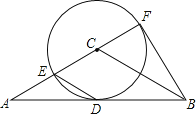
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌACЃНBCЃЌABЪЧЁбCЕФЧаЯпЃЌЧаЕуЮЊЕуDЃЌжБЯпACНЛЁбCгкЕуEЁЂFЃЌЧвCF=![]() ACЃЌ
ACЃЌ
ЃЈ1ЃЉЧѓжЄЃКЁїABFЪЧжБНЧШ§НЧаЮЃЎ
ЃЈ2ЃЉШєACЃН6ЃЌдђжБНгЛиД№BFЕФГЄЪЧЖрЩйЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌABЁЮDCЃЌABЃНADЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌACЦНЗжЁЯBADЃЌЙ§ЕуCзїCEЁЭABНЛABЕФбгГЄЯпгкЕуEЃЌСЌНгOEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧСтаЮЃЛ
ЃЈ2ЃЉШєABЃН![]() ЃЌBDЃН2ЃЌЧѓOEЕФГЄЃЎ
ЃЌBDЃН2ЃЌЧѓOEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
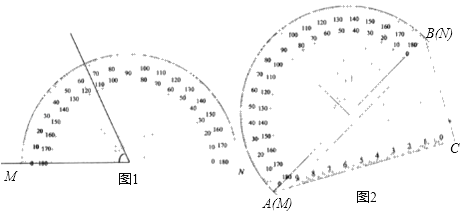
ЁОЬтФПЁПШчЭМ1ЃЌЪЧгУСПНЧЦївЛИіНЧЕФВйзїЪОвтЭМЃЌСПНЧЦїЕФЖСЪ§ДгMЕуПЊЪМЃЈМДMЕуЕФЖСЪ§ЮЊ0ЃЉЃЌШчЭМ2ЃЌАбетИіСПНЧЦїгывЛПщ30ЁуЃЈЁЯCABЃН30ЁуЃЉНЧЕФШ§НЧАхЦДдквЛЦ№ЃЌШ§НЧАхЕФаББпABгыСПНЧЦїЫљдкдВЕФжБОЖMNжиКЯЃЌЯжгаЩфЯпCШЦЕуCДгCAПЊЪМбиЫГЪБеыЗНЯђвдУПУы2ЁуЕФЫйЖШа§зЊЕНгыCBЃЌдка§зЊЙ§ГЬжаЃЌЩфЯпCPгыСПНЧЦїЕФАыдВЛЁНЛгкEЃЎСЌНгBEЃЎ
ЃЈ1ЃЉЕБЩфЯпCPОЙ§ABЕФжаЕуЪБЃЌЕуEДІЕФЖСЪ§ЪЧЁЁ ЁЁЃЌДЫЪБЁїBCEЕФаЮзДЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉЩша§зЊxУыКѓЃЌЕуEДІЕФЖСЪ§ЮЊyЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБCPа§зЊЖрЩйУыЪБЃЌЁїBCEЪЧЕШбќШ§НЧаЮЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌBCЃН2ABЃЌEЃЌFЗжБ№ЪЧBCЃЌADЕФжаЕуЃЌAEЃЌBFНЛгкЕуOЃЌСЌНгEFЃЌOCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABEFЪЧСтаЮЃЛЃЈ2ЃЉШєBCЃН8ЃЌЁЯABCЃН60ЁуЃЌЧѓOCЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњПЮЭтдФЖСЧщПіЃЌОЭбЇЩњУПжмдФЖСЪБМфЫцЛњЕїВщСЫВПЗжбЇЩњЃЌЕїВщНсЙћАДадБ№ећРэШчЯТЃК
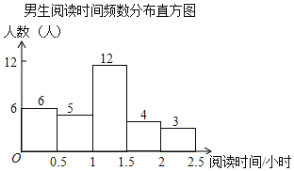
ХЎЩњдФЖСЪБМфШЫЪ§ЭГМЦБэ
дФЖСЪБМф | ШЫЪ§ | еМХЎЩњШЫЪ§АйЗжБШ |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
ИљОнЭМБэНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкХЎЩњдФЖСЪБМфШЫЪ§ЭГМЦБэжаЃЌ![]() ЁЁ ЃЌ
ЁЁ ЃЌ![]() ЁЁ ЃЛ
ЁЁ ЃЛ
ЃЈ2ЃЉДЫДЮГщбљЕїВщжаЃЌЙВГщШЁСЫЁЁ УћбЇЩњЃЌбЇЩњдФЖСЪБМфЕФжаЮЛЪ§дкЁЁ ЪБМфЖЮЃЛ
ЃЈ3ЃЉДгдФЖСЪБМфдк2ЁЋ2.5аЁЪБЕФ5УћбЇЩњжаЫцЛњГщШЁ2УћбЇЩњВЮМгЪаМЖдФЖСЛюЖЏЃЌЧЁКУГщЕНФаХЎЩњИївЛУћЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com