
【题目】小李同学根据6位同学在一次数学测试中的成绩绘制了一条形统计图(如图).
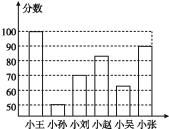
(1)哪位同学的分数最高,哪位同学的分数最低,他们相差多少?
(2)小张的分数是小孙分数的几倍?
(3)这个图易使人产生错误的感觉吗?为什么?
(4)为了更为直观、清楚地反映这6名同学的分数状况,这个图应做怎样的改动?
【答案】(1)小王的分数最高,为100分;小孙的分数最低,为50分;两人分数相差50分;(2)1.8倍;(3)易产生错误的感觉;理由见解析;(4)见解析.
【解析】
(1)由条形统计图可以看出:小王的分数最高,为100分;小孙的分数最低,为50分;然后得出两人分数相差多少
(2)由条形统计图可以看出:小张的分数为90分,小孙的分数为50分,然后得出小张的分数是小孙分数的倍数即可
(3)看纵坐标的分数段的划分应该是10分一段,但从原点到50段是50分一段,这样易产生错误的感觉;而且没按分数的一定顺序排列;
(4)为了更为直观、清楚地反映这5名同学的分数状况,这个图应该改动,方法:①从左至右按成绩从高到低的顺序排列,②将分数段重新划分,而且至少应加出5分的分数段
解:(1)小王的分数最高,为100分;小孙的分数最低,为50分;两人分数相差100-50=50分.
(2) 小张的分数为90分,小孙的分数为50分,小张的分数是小孙分数的倍数为![]() =1.8(倍).
=1.8(倍).
(3)易产生错误的感觉.因为没按分数的一定顺序排列;分数段划分不细,估计值易出错.
(4)改动方法:①从左至右按小孙、小吴、小刘、小赵、小张、小王的顺序排列;
②将分数段重新划分,而且至少应加出55、65、75、85、95的分数段.


科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当四边形MENF是正方形时,求AD:AB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AFAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
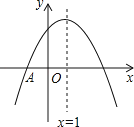
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,小明家把一步行台阶由倾角45°改为倾角为30°,已知原台阶坡面AB的长为5m(BC所在地面为水平面),结果准确到0.1m,参考数据:![]() ,
,![]()
(1)改后的台阶坡面会加长多少?
(2)改好的台阶多占多长一段水平地面?

查看答案和解析>>
科目:初中数学 来源: 题型:
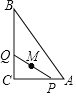
【题目】我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹,如图,在Rt△ABC中,∠C=90°,AC=8,BC=12,动点P从点A开始沿射线AC方向以1个单位秒的速度向点C运动,动点Q从点C开始沿射线CB方向以2个单位/秒的速度向点运动,P、Q两点分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M运动的轨迹长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
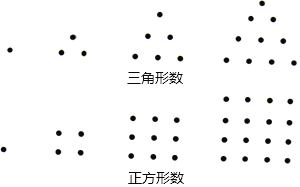
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
A. 33 B. 301 C. 386 D. 571
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
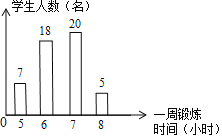
A.平均数是6
B.中位数是6.5
C.众数是7
D.平均每周锻炼超过6小时的人数占该班人数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y![]() bx+c,经过点A(1,3)、B(0,1),过点A作x轴的平行线交抛物线于另一点C
bx+c,经过点A(1,3)、B(0,1),过点A作x轴的平行线交抛物线于另一点C
(1)求抛物线的表达式及其顶点坐标;
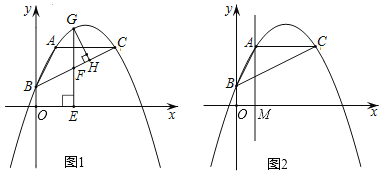
(2)如图1,点G是BC上方抛物线上的一个动点,分别过点G作GH⊥BC于点H、作GE⊥x轴于点E,交BC于点F,在点G运动的过程中,△GFH的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图2,过A点的直线垂直x轴于点M,点N为直线AM上任意一点,当△BCN为直角三角形时,请直接写出点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com