
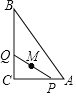
【题目】我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹,如图,在Rt△ABC中,∠C=90°,AC=8,BC=12,动点P从点A开始沿射线AC方向以1个单位秒的速度向点C运动,动点Q从点C开始沿射线CB方向以2个单位/秒的速度向点运动,P、Q两点分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M运动的轨迹长为__.
【答案】3![]() .
.
【解析】
先以C为原点,以AC所在直线为x轴,建立平面直角坐标系,由题意知0≤t≤6,求得t=0及t=6时M的坐标,得到直线M1M2的解析式为y=﹣2x+8.过点M2作M2N⊥x轴于点N,则M2N=6,M1N=3,M1M2=3![]() ,线段PQ中点M所经过的路径长为3
,线段PQ中点M所经过的路径长为3![]() 个单位长度.
个单位长度.
以C为原点,以AC所在直线为x轴,建立平面直角坐标系:
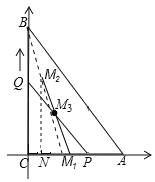
依题意,可知0≤t≤6,当t=0时,点M1的坐标为(4,0);
当t=6时,点M2的坐标为(1,6),
设直线M1M2的解析式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴直线M1M2的解析式为y=﹣2x+8.
设动点运动的时间为t秒,
则有点Q(0,2t),P(8﹣t,0),
∴在运动过程中,线段PQ中点M3的坐标为(![]() ,t),
,t),
把x=![]() 代入y=﹣2x+8,得y=﹣2×
代入y=﹣2x+8,得y=﹣2×![]() +8=t,
+8=t,
∴点M3在M1M2直线上,
过点M2作M2N⊥x轴于点N,则M2N=6,M1N=3,
∴M1M2=3![]() ,
,
∴线段PQ中点M所经过的路径长为3![]() 个单位长度.
个单位长度.
故答案为:3![]() .
.


科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣3x+k=0有实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程(m﹣1)x2+x+m﹣3=0与方程x2﹣3x+k=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李同学根据6位同学在一次数学测试中的成绩绘制了一条形统计图(如图).
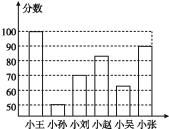
(1)哪位同学的分数最高,哪位同学的分数最低,他们相差多少?
(2)小张的分数是小孙分数的几倍?
(3)这个图易使人产生错误的感觉吗?为什么?
(4)为了更为直观、清楚地反映这6名同学的分数状况,这个图应做怎样的改动?
查看答案和解析>>
科目:初中数学 来源: 题型:
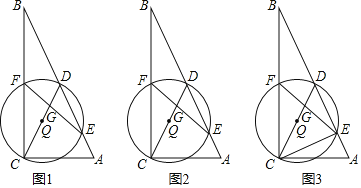
【题目】已知:在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点,以CD为直径的⊙Q分别交BC、BA于点F、E,点E位于点D下方,连接EF交CD于点G.
(1)如图1,如果BC=2,求DE的长;
(2)如图2,设BC=x,![]() =y,求y关于x的函数关系式及其定义域;
=y,求y关于x的函数关系式及其定义域;
(3)如图3,连接CE,如果CG=CE,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省开封市铁塔始建于公元1049年(北宋皇祐元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明在铁塔一侧的水平面上一个台阶的底部A处测得塔顶P的仰角为45°,走到台阶顶部B处,又测得塔顶P的仰角为38.7°,已知台阶的总高度BC为3米,总长度AC为10米,试求铁塔的高度.(结果精确到1米,参考数据:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)
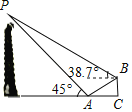
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某风景区内有一瀑布,AB表示瀑布的垂直高度,在与瀑布底端同一水平位置的点D处测得瀑布顶端A的仰角β为45°,沿坡度i=1:3的斜坡向上走100米,到达观景台C,在C处测得瀑布顶端A的仰角α为37°,若点B、D、E在同一水平线上.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈3.16)
≈3.16)
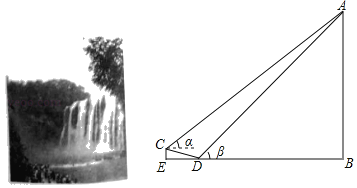
(1)观景台的高度CE为 米(结果保留准确值);
(2)求瀑布的落差AB(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com