
°æƒø°ø∫”ƒœ °ø™∑‚ –Ã˙À˛ ºΩ®”⁄π´‘™1049ƒÍ£®±±ÀŒª µv‘™ƒÍ£©£¨ «π˙º“÷ÿµ„±£ª§ŒƒŒÔ÷Æ“ª£¨‘⁄900∂ýƒÍ÷–£¨¿˙æ≠¡À ˝¥Œµÿ’°¢¥Û∑Á°¢Àƪº∂¯Œ°»ª“Ÿ¡¢£¨Àÿ”–°∞ÃÏœ¬µ⁄“ªÀ˛°±÷Æ≥∆£Æ»ÁÕº£¨–°√˜‘⁄Ã˙À˛“ª≤ýµƒÀÆ∆Ω√Ê…œ“ª∏ˆÃ®Ω◊µƒµ◊≤øA¥¶≤‚µ√À˛∂•Pµƒ—ˆΩ«Œ™45°„£¨◊þµΩîΩ◊∂•≤øB¥¶£¨”÷≤‚µ√À˛∂•Pµƒ—ˆΩ«Œ™38.7°„£¨“—÷™Ã®Ω◊µƒ◊Ð∏þ∂»BCŒ™3√◊£¨◊Ð≥§∂»ACŒ™10√◊£¨ ‘«ÛÃ˙À˛µƒ∏þ∂»£Æ£®Ω·π˚æ´»∑µΩ1√◊£¨≤Œøº ˝æð£∫sin38.7°„°÷0.63£¨cos38.7°„°÷0.78£¨tan38.7°„°÷0.80£©
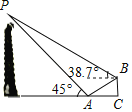
°æ¥∞∏°øÃ˙À˛‘º∏þ55√◊£Æ
°æΩ‚Œˆ°ø
»ÁÕº£¨π˝µ„B◊˜BE°ÕDP”⁄µ„E£¨”…Âø…÷™£¨°œEBP£Ω38.7°„£¨°œDAF£Ω45°„£¨BE£ΩCD£¨DP£ΩAD£¨…ËÃ˙À˛∏þ∂»DPŒ™x√◊£¨‘ÚBE£ΩCD£Ωx+10£¨Ω‚÷±Ω«»˝Ω«–Œº¥ø…µ√µΩΩ·¬€£Æ
»ÁÕº£¨π˝µ„B◊˜BE°ÕDP”⁄µ„E£¨
”…Âø…÷™£¨°œEBP£Ω38.7°„£¨°œDAF£Ω45°„£¨BE£ΩCD£¨DP£ΩAD£¨
…ËÃ˙À˛∏þ∂»DPŒ™x√◊£¨‘ÚBE£ΩCD£Ωx+10£¨
EP£ΩDP©ÅDE£ΩAD©ÅBC£Ωx©Å3£¨
‘⁄Rt°˜BEP÷–°þEP£Ωx©Å3£¨BE£Ωx+10£¨
°ýtan°œEBP£Ω![]() £¨x©Å3£Ω£®x+10£©°¡tan38.7°„£¨
£¨x©Å3£Ω£®x+10£©°¡tan38.7°„£¨
Ω‚µ√x£Ω55£¨
¥£∫Ã˙À˛‘º∏þ55√◊£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
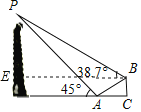
°æƒø°ø¡Ò¡´…œ –µƒ ±∫Ú£¨ƒ≥ÀÆπ˚––“‘°∞œþ…œ°±”ΰ∞œþœ¬°±œýΩ·∫œµƒ∑Ω Ω“ªπ≤œ˙ €¡À![]() œ‰¡Ò¡´£Æ“—÷™°∞œþ…œ°±œ˙ €µƒ√øœ‰¿˚»ÛŒ™
œ‰¡Ò¡´£Æ“—÷™°∞œþ…œ°±œ˙ €µƒ√øœ‰¿˚»ÛŒ™![]() ‘™£Æ°∞œþœ¬°±œ˙ €µƒ√øœ‰¿˚»Û
‘™£Æ°∞œþœ¬°±œ˙ €µƒ√øœ‰¿˚»Û![]() £®‘™£©”Îœ˙ €¡ø
£®‘™£©”Îœ˙ €¡ø![]() £®œ‰£©
£®œ‰£©![]() ÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕº÷–µƒœþ∂Œ
÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕº÷–µƒœþ∂Œ![]() £Æ
£Æ
£®1£©«Û![]() ”Î
”Î![]() ÷ƺ‰µƒ∫Ø ˝πÿœµ£Æ
÷ƺ‰µƒ∫Ø ˝πÿœµ£Æ
£®2£©µ±°∞œþœ¬°±µƒœ˙ €¿˚»ÛŒ™![]() ‘™ ±£¨«Û
‘™ ±£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
£®3£© µº °∞œþœ¬°±œ˙ € ±£¨√øœ‰ªπ“™÷ß≥ˆ∆‰À¸∑—”√![]() ‘™
‘™![]() £¨»Ù°∞œþ…œ°±”ΰ∞œþœ¬°± €ÕÍ’‚
£¨»Ù°∞œþ…œ°±”ΰ∞œþœ¬°± €ÕÍ’‚![]() œ‰¡Ò¡´À˘ªÒµ√µƒ◊Ó¥Û◊п˚»ÛŒ™
œ‰¡Ò¡´À˘ªÒµ√µƒ◊Ó¥Û◊п˚»ÛŒ™![]() ‘™£¨«Û
‘™£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
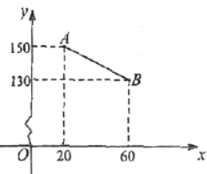
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“—÷™≈◊ŒÔœþy£Ωax2+bx©Å5”Îx÷·Ωª”⁄A£®©Å1£¨0£©£¨B£®5£¨0£©¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£Æ
£®1£©«Û≈◊ŒÔœþµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©»ÁÕº2£¨CE°Œx÷·”Î≈◊ŒÔœþœýΩª”⁄µ„E£¨µ„H «÷±œþCEœ¬∑Ω≈◊ŒÔœþ…œµƒ∂ص„£¨π˝µ„H«“”Îy÷·∆Ω––µƒ÷±œþ”ÎBC£¨CE∑÷±œýΩª”⁄µ„F£¨G£¨ ‘ÃΩæøµ±µ„H‘À∂صΩ∫Œ¥¶ ±£¨Àƒ±þ–ŒCHEFµƒ√ʪ˝◊Ó¥Û£¨«Ûµ„Hµƒ◊¯±Í£ª
£®3£©»Ùµ„KŒ™≈◊ŒÔœþµƒ∂•µ„£¨µ„M£®4£¨m£© «∏√≈◊ŒÔœþ…œµƒ“ªµ„£¨‘⁄x÷·£¨y÷·…œ∑÷±’“µ„P£¨Q£¨ πÀƒ±þ–ŒPQKMµƒ÷Ð≥§◊Ó–°£¨«Û≥ˆµ„P£¨Qµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À¡ÀΩ‚—ß…˙πÿ◊¢»»µ„–¬Œ≈µƒ«Èøˆ£¨°∞¡Ωª·°±∆⁄º‰£¨–°√˜∂‘∞ýº∂Õ¨—ß“ª÷Ѓ⁄ ’ø¥°∞¡Ωª·°±–¬Œ≈µƒ¥Œ ˝«Èøˆ◊˜¡Àµ˜≤È£¨µ˜≤ÈΩ·π˚Õ≥º∆»ÁÕºÀ˘ 森∆‰÷–ƒ–…˙ ’ø¥![]() ¥Œµƒ»À ˝√ª”–±Í≥ˆ£©.
¥Œµƒ»À ˝√ª”–±Í≥ˆ£©.
∏˘æð…œ ˆ–≈œ¢£¨Ω‚¥œ¬¡–∏˜Ã‚£∫
 °¡
°¡
£®1£©∏√∞ýº∂≈Æ…˙»À ˝ «__________£¨≈Æ…˙ ’ø¥°∞¡Ωª·°±–¬Œ≈¥Œ ˝µƒ÷–Œª ˝ «________£ª
£®2£©∂‘”⁄ƒ≥∏ˆ»∫㨌“√«∞—“ª÷Ѓ⁄ ’ø¥ƒ≥»»µ„–¬Œ≈¥Œ ˝≤ªµÕ”⁄![]() ¥Œµƒ»À ˝’º∆‰À˘‘⁄»∫ÃÂ◊лÀ ˝µƒ∞Ÿ∑÷±»Ω–◊ˆ∏√»∫ÃÂ∂‘ƒ≥»»µ„–¬Œ≈µƒ°∞πÿ◊¢÷∏ ˝°±.»Áπ˚∏√∞ýº∂ƒ–…˙∂‘°∞¡Ωª·°±–¬Œ≈µƒ°∞πÿ◊¢÷∏ ˝°±±»≈Æ…˙µÕ
¥Œµƒ»À ˝’º∆‰À˘‘⁄»∫ÃÂ◊лÀ ˝µƒ∞Ÿ∑÷±»Ω–◊ˆ∏√»∫ÃÂ∂‘ƒ≥»»µ„–¬Œ≈µƒ°∞πÿ◊¢÷∏ ˝°±.»Áπ˚∏√∞ýº∂ƒ–…˙∂‘°∞¡Ωª·°±–¬Œ≈µƒ°∞πÿ◊¢÷∏ ˝°±±»≈Æ…˙µÕ![]() £¨ ‘«Û∏√∞ýº∂ƒ–…˙»À ˝£ª
£¨ ‘«Û∏√∞ýº∂ƒ–…˙»À ˝£ª
£®3£©Œ™Ω¯“ª≤Ω∑÷Œˆ∏√∞ýº∂ƒ–°¢≈Æ…˙ ’ø¥°∞¡Ωª·°±–¬Œ≈¥Œ ˝µƒÃÿµ„£¨–°√˜∏¯≥ˆ¡Àƒ–…˙µƒ≤ø∑÷Õ≥º∆¡ø£®»Á±Ì£©.
Õ≥º∆¡ø | ∆Ωæ˘ ˝£®¥Œ£© | ÷–Œª ˝£®¥Œ£© | ÷⁄ ˝£®¥Œ£© | ∑Ω≤Ó | °≠ |
∏√∞ýº∂ƒ–…˙ |
|
|
|
| °≠ |
∏˘æðƒ„À˘—ßπ˝µƒÕ≥º∆÷™ ∂£¨ µ±º∆À„≈Æ…˙µƒ”–πÿÕ≥º∆¡ø£¨Ω¯∂¯±»Ωœ∏√∞ýº∂ƒ–°¢≈Æ…˙ ’ø¥°∞¡Ωª·°±–¬Œ≈¥Œ ˝µƒ≤®∂Ø¥Û–°.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨AB=10£¨AC=8£¨BC=6£¨÷±œþlæ≠π˝µ„A£¨«“¥π÷±”⁄AB£¨∑÷±”ÎAB°¢ACœýΩª”⁄µ„M£¨N£Æ÷±œþl¥”µ„A≥ˆ∑¢£¨—ÿAB∑ΩœÚ“‘1cm/sµƒÀŸ∂»œÚµ„B‘À∂Ø£¨µ±÷±œþlæ≠π˝µ„B ±Õ£÷π‘À∂Ø£¨»Ù‘À∂Øπ˝≥Ã÷–°˜AMNµƒ√ʪ˝ «y(cm2)£¨÷±œþlµƒ‘À∂Ø ±º‰ «x(s)‘Úy”Îx÷ƺ‰∫Ø ˝πÿœµµƒÕºœÛ¥Û÷¬ «( )
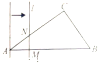
A.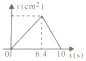 B.
B.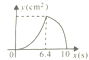
C.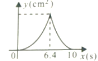 D.
D.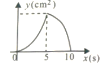
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄æÿ–ŒABCD÷–£¨AB=3£¨AD=5£¨µ„E‘⁄DC…œ£¨Ω´æÿ–ŒABCD—ÿAE’€µ˛£¨µ„D«°∫√¬‰‘⁄BC±þ…œµƒµ„F¥¶£¨ƒ«√¥sin°œEFCµƒ÷µŒ™______£Æ
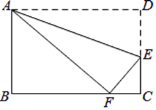
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
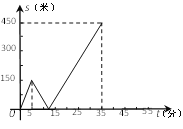
°æƒø°øº◊““¡Ω»À‘»ÀŸ¥”Õ¨“ªµÿµ„µΩ1500√◊¥¶µƒÕº Èπðø¥ È£¨º◊≥ˆ∑¢5∑÷÷”∫Û£¨“““‘50√◊/∑÷µƒÀŸ∂»—ÿÕ¨“ª¬∑œþ––◊þ.…˺◊““¡Ω»Àœýæý![]() £®√◊£©£¨º◊––◊þµƒ ±º‰Œ™
£®√◊£©£¨º◊––◊þµƒ ±º‰Œ™![]() £®∑÷£©£¨
£®∑÷£©£¨![]() πÿ”⁄
πÿ”⁄![]() µƒ∫Ø ˝∫Ø ˝ÕºœÒµƒ“ª≤ø∑÷»ÁÕºÀ˘ æ.
µƒ∫Ø ˝∫Ø ˝ÕºœÒµƒ“ª≤ø∑÷»ÁÕºÀ˘ æ.
£®1£©«Ûº◊––◊þµƒÀŸ∂»£ª
£®2£©‘⁄◊¯±Íœµ÷–£¨≤πª≠![]() πÿ”⁄
πÿ”⁄![]() ∫Ø ˝ÕºœÛµƒ∆‰”ý≤ø∑÷£ª
∫Ø ˝ÕºœÛµƒ∆‰”ý≤ø∑÷£ª
£®3£©Œ º◊°¢““¡Ω»À∫Œ ±œýæý360√◊£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÕº1 «“ªÃ® µŒÔÕ∂”∞“«£¨Õº2 «À¸µƒ æ“‚Õº£¨’€œþO©ÅA©ÅB©ÅC±Ì æ÷ߺУ¨÷ߺеƒ“ª≤ø∑÷O©ÅA©ÅB «πÃ∂®µƒ£¨¡Ì“ª≤ø∑÷BC «ø…–˝◊™µƒ£¨œþ∂ŒCD±Ì æÕ∂”∞ÃΩÕ∑£¨OM±Ì æÀÆ∆Ω◊¿√Ê£¨AO°ÕOM£¨¥π◊„Œ™µ„O£¨«“AO£Ω7cm£¨°œBAO£Ω160°„£¨BC°ŒOM£¨CD£Ω8cm£Æ
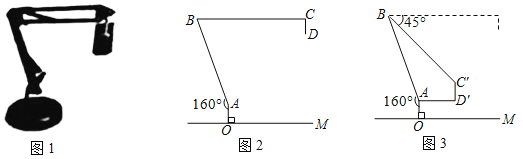
Ω´Õº2÷–µƒBC»∆µ„BœÚœ¬–˝◊™45°„£¨ πµ√BCD¬‰‘⁄BC°‰D°‰µƒŒª÷√£®»ÁÕº3À˘ 棩£¨¥À ±C°‰D°‰°ÕOM£¨AD°‰°ŒOM£¨AD°‰£Ω16cm£¨«Ûµ„BµΩÀÆ∆Ω◊¿√ÊOMµƒæý¿Î£¨£®≤Œøº ˝æð£∫sin70°„°÷0.94£¨cos70°„°÷0.34£¨cot70°„°÷0.36£¨Ω·π˚æ´»∑µΩ1cm£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øRt°˜ABC÷–£¨AB£ΩAC£¨Dµ„Œ™Rt°˜ABCÕ‚“ªµ„£¨«“BD°ÕCD£¨DFŒ™°œBDAµƒ∆Ω∑÷œþ£¨µ±°œACD£Ω15°„£¨œ¬¡–Ω·¬€£∫¢Ÿ°œADC£Ω45°„£ª¢⁄AD£ΩAF£ª¢€AD+AF£ΩBD£ª¢ÐBC©ÅCE£Ω2D,∆‰÷–’˝»∑µƒ «( )

A.¢Ÿ¢€B.¢Ÿ¢⁄¢ÐC.¢Ÿ¢€¢ÐD.¢Ÿ¢⁄¢€¢Ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com