
°æƒø°ø»ÁÕº£¨ƒ≥∑Áæ∞«¯ƒ⁄”–“ª∆Ÿ≤º£¨AB±Ì æ∆Ÿ≤ºµƒ¥π÷±∏þ∂»£¨‘⁄”Î∆Ÿ≤ºµ◊∂ÀÕ¨“ªÀÆ∆ΩŒª÷√µƒµ„D¥¶≤‚µ√∆Ÿ≤º∂•∂ÀAµƒ—ˆΩ«¶¬Œ™45°„£¨—ÿ∆¬∂»i£Ω1£∫3µƒ–±∆¬œÚ…œ◊þ100√◊£¨µΩ¥Ôπ€æ∞îC£¨‘⁄C¥¶≤‚µ√∆Ÿ≤º∂•∂ÀAµƒ—ˆΩ«¶¡Œ™37°„£¨»Ùµ„B°¢D°¢E‘⁄Õ¨“ªÀÆ∆Ωœþ…œ£Æ£®≤Œøº ˝æð£∫sin37°„°÷0.6£¨cos37°„°÷0.8£¨tan37°„°÷0.75£¨![]() °÷1.41£¨
°÷1.41£¨![]() °÷3.16£©
°÷3.16£©
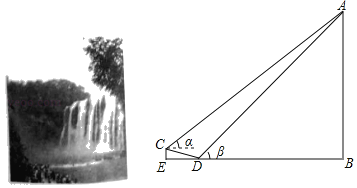
£®1£©π€æ∞∏þ∂»CEŒ™°° °°√◊£®Ω·π˚±£¡Ù◊º»∑÷µ£©£ª
£®2£©«Û∆Ÿ≤ºµƒ¬‰≤ÓAB£®Ω·π˚±£¡Ù’˚ ˝£©£Æ
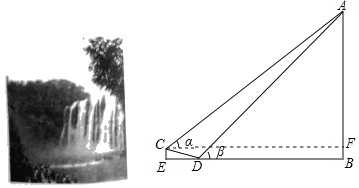
°æ¥∞∏°ø£®1£©10![]() £ª£®2£©∆Ÿ≤ºµƒ¬‰≤Ó‘ºŒ™411√◊£Æ
£ª£®2£©∆Ÿ≤ºµƒ¬‰≤Ó‘ºŒ™411√◊£Æ
°æΩ‚Œˆ°ø
£®1£©Õ®π˝Ω‚÷±Ω«°˜CDEµ√µΩ£∫CE£ΩCDsin37°„£Æ
£®2£©◊˜CF°ÕAB”⁄F£¨ππ‘Ïæÿ–ŒCEBF£Æ”…æÿ–Œµƒ–‘÷ ∫ÕΩ‚÷±Ω«°˜ADBµ√µΩDEµƒ≥§∂»£¨◊Ó∫ÛÕ®π˝Ω‚÷±Ω«°˜ACF«Ûµ√¥∞∏£Æ
£®1£©°þtan°œCDE£Ω![]()
°ýCD£Ω3CE£Æ
”÷CD£Ω100√◊£¨
°ý100£Ω![]()
°ýCE£Ω10![]() £Æ
£Æ
π ¥∞∏ «£∫10![]() £Æ
£Æ
£®2£©◊˜CF°ÕAB”⁄F£¨‘ÚÀƒ±þ–ŒCEBF «æÿ–Œ£Æ
°ýCE£ΩBF£Ω10![]() £¨CF£ΩBE£Æ
£¨CF£ΩBE£Æ
‘⁄÷±Ω«°˜ADB÷–£¨°œDB£Ω45°„£Æ…ËAB£ΩBD£Ωx√◊£Æ
°þ![]() £Ω
£Ω![]() £¨
£¨
°ýDE£Ω30![]() £Æ
£Æ
‘⁄÷±Ω«°˜ACF÷–£¨°œACF£Ω37°„£¨tan°œACF![]()
Ω‚µ√x°÷411£Æ
¥£∫∆Ÿ≤ºµƒ¬‰≤Ó‘ºŒ™411√◊£Æ


 ”≈º”æ´æÌœµ¡–¥∞∏
”≈º”æ´æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() «
«![]() µƒ÷±æ∂£¨µ„
µƒ÷±æ∂£¨µ„![]() «ª°
«ª°![]() …œ“ªµ„£¨«“
…œ“ªµ„£¨«“![]() £¨
£¨![]() ”Î
”Î![]() Ωª”ε„
Ωª”ε„![]() £Æ
£Æ
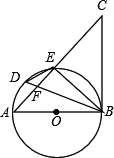
(1)«Û÷§£∫![]() «
«![]() µƒ«–œþ£ª
µƒ«–œþ£ª
(2)»Ù![]() ∆Ω∑÷
∆Ω∑÷![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £ª
£ª
(3)‘⁄(2)µƒÃıº˛œ¬£¨—”≥§![]() £¨
£¨![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨»Ù
£¨»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ≥§∫Õ
µƒ≥§∫Õ![]() µƒ∞Îæ∂£Æ
µƒ∞Îæ∂£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂ÀŒÁΩ⁄ «Œ“π˙µƒ¥´Õ≥Ω⁄»’£¨»À√«Àÿ”–≥‘Ù’◊”µƒœ∞À◊£¨ƒ≥…Ã≥°‘⁄∂ÀŒÁΩ⁄¿¥¡Ÿ÷ƺ ”√3000‘™π∫Ω¯![]() °¢
°¢![]() ¡Ω÷÷Ù’◊”1100∏ˆ£¨π∫¬Ú
¡Ω÷÷Ù’◊”1100∏ˆ£¨π∫¬Ú![]() ÷÷Ù’◊””Îπ∫¬Ú
÷÷Ù’◊””Îπ∫¬Ú![]() ÷÷Ù’◊”µƒ∑—”√œýÕ¨£¨“—÷™
÷÷Ù’◊”µƒ∑—”√œýÕ¨£¨“—÷™![]() Ù’◊”µƒµ•º€ «
Ù’◊”µƒµ•º€ «![]() ÷÷Ù’◊”µ•º€µƒ1.2±∂.
÷÷Ù’◊”µ•º€µƒ1.2±∂.
£®1£©«Û![]() °¢
°¢![]() ¡Ω÷÷Ù’◊”µƒµ•º€∏˜ «∂ý…Ÿ£ø
¡Ω÷÷Ù’◊”µƒµ•º€∏˜ «∂ý…Ÿ£ø
£®2£©»Ùº∆ªÆ”√≤ª≥¨π˝7000‘™µƒ◊ Ω‘Ÿ¥Œπ∫¬Ú![]() °¢
°¢![]() ¡Ω÷÷Ù’◊”π≤2600∏ˆ£¨“—÷™
¡Ω÷÷Ù’◊”π≤2600∏ˆ£¨“—÷™![]() °¢
°¢![]() ¡Ω÷÷Ù’◊”µƒΩ¯º€≤ª±‰£¨«Û
¡Ω÷÷Ù’◊”µƒΩ¯º€≤ª±‰£¨«Û![]() ÷–Ù’◊”◊Ó∂ýƒÐπ∫Ω¯∂ý…Ÿ∏ˆ£ø
÷–Ù’◊”◊Ó∂ýƒÐπ∫Ω¯∂ý…Ÿ∏ˆ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº «≈◊ŒÔœþy=ax2+bx+c£®a°Ÿ0£©µƒ≤ø∑÷ÕºœÛ£¨∆‰∂•µ„◊¯±ÍŒ™£®1£¨n£©£¨«“”Îx÷·µƒ“ª∏ˆΩªµ„‘⁄µ„£®3£¨0£©∫Õ£®4£¨0£©÷ƺ‰£Æ‘Úœ¬¡–Ω·¬€£∫¢Ÿa©Åb+c£æ0£ª¢⁄3a+b=0£ª¢€b2=4a£®c©Ån£©£ª¢Ð“ª‘™∂˛¥Œ∑Ω≥Ãax2+bx+c=n©Å1”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝∏˘£Æ∆‰÷–’˝»∑Ω·¬€µƒ «______________£®÷ªÃÓ–Ú∫≈£©

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄–°’˝∑Ω–Œ◊È≥…Õ¯∏ÒÕº÷–£¨Àƒ±þ–Œ ABCD µƒ∂•µ„∂º‘⁄∏Òµ„…œ£¨»ÁÕºÀ˘ æ£Æ‘Úœ¬¡–Ω·¬€¥Ì ŒÛµƒ «£® £©
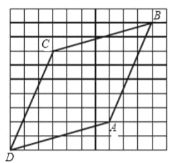
A.![]() B.
B.![]()
C.Àƒ±þ–Œ![]() «¡‚–ŒD.Ω´±þ
«¡‚–ŒD.Ω´±þ![]() œÚ”“∆Ω“∆
œÚ”“∆Ω“∆![]() ∏Ò£¨‘ŸœÚ…œ∆Ω“∆
∏Ò£¨‘ŸœÚ…œ∆Ω“∆![]() ∏ÒæՔαþ
∏ÒæՔαþ![]() ÷ÿ∫œ
÷ÿ∫œ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°œAOB£Ω45°„£¨π˝OA…œµΩµ„Oµƒæý¿Î∑÷±Œ™1£¨3£¨5£¨7£¨9£¨11£¨µƒµ„◊˜OAµƒ¥πœþ”ÎOBœýΩª£¨µ√µΩ≤¢±Í≥ˆ“ª◊È∫⁄…´Ã𖌣¨À¸√«µƒ√ʪ˝∑÷±Œ™S1£¨S2£¨S3£¨S4£¨°≠£¨π€≤ÏÕº÷–µƒπʬ…£¨«Û≥ˆµ⁄10∏ˆ∫⁄…´Ã𖌵ƒ√ʪ˝S10£Ω_____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() «±þ≥§Œ™
«±þ≥§Œ™![]() µƒµ»±þ»˝Ω«–Œ£¨
µƒµ»±þ»˝Ω«–Œ£¨![]() Œ™
Œ™![]() ±þ…œµƒ∏þ£¨“‘
±þ…œµƒ∏þ£¨“‘![]() Œ™±þ◊˜µ»±þ»˝Ω«–Œ
Œ™±þ◊˜µ»±þ»˝Ω«–Œ![]() £¨
£¨![]() Œ™
Œ™![]() ÷–µ„£¨‘Úœþ∂Œ
÷–µ„£¨‘Úœþ∂Œ![]() µƒ≥§Œ™__.
µƒ≥§Œ™__.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂‘”⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–µƒµ„
÷–µƒµ„![]() ∫Õ
∫Õ![]() £®∞Îæ∂Œ™
£®∞Îæ∂Œ™![]() £©£¨∏¯≥ˆ»Áœ¬∂®“£∫»Ùµ„
£©£¨∏¯≥ˆ»Áœ¬∂®“£∫»Ùµ„![]() πÿ”⁄µ„
πÿ”⁄µ„![]() µƒ∂‘≥∆µ„Œ™
µƒ∂‘≥∆µ„Œ™![]() £¨«“
£¨«“![]() £¨‘Ú≥∆µ„
£¨‘Ú≥∆µ„![]() Œ™
Œ™![]() µƒ≥∆–ƒµ„£Æ
µƒ≥∆–ƒµ„£Æ
£®1£©µ±![]() µƒ∞Îæ∂Œ™2 ±£¨
µƒ∞Îæ∂Œ™2 ±£¨
¢Ÿ»ÁÕº1£¨‘⁄µ„![]() £¨
£¨![]() £¨
£¨![]() ÷–£¨
÷–£¨![]() µƒ≥∆–ƒµ„ « £ª
µƒ≥∆–ƒµ„ « £ª
¢⁄»ÁÕº2£¨µ„![]() ‘⁄÷±œþ
‘⁄÷±œþ![]() …œ£¨»Ùµ„
…œ£¨»Ùµ„![]() «
«![]() µƒ≥∆–ƒµ„£¨«Ûµ„
µƒ≥∆–ƒµ„£¨«Ûµ„![]() µƒ∫·◊¯±Í
µƒ∫·◊¯±Í![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®2£©![]() µƒ‘≤–ƒŒ™
µƒ‘≤–ƒŒ™![]() £¨∞Îæ∂Œ™2£¨÷±œþ
£¨∞Îæ∂Œ™2£¨÷±œþ![]() ”Î
”Î![]() ÷·£¨
÷·£¨![]() ÷·∑÷±Ωª”⁄µ„
÷·∑÷±Ωª”⁄µ„![]() £¨
£¨![]() £Æ»Ùœþ∂Œ
£Æ»Ùœþ∂Œ![]() …œµƒÀ˘”–µ„∂º «
…œµƒÀ˘”–µ„∂º «![]() µƒ≥∆–ƒµ„£¨÷±Ω”–¥≥ˆ
µƒ≥∆–ƒµ„£¨÷±Ω”–¥≥ˆ![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À∞Ô÷˙ –ƒ⁄“ª√˚ªº°∞∞◊—™≤°°±µƒ÷–—ß…˙£¨∂´”™ –ƒ≥—ß–£ ˝—ß…ÁÕ≈15√˚Õ¨—ߪ˝º´æËøÓ£¨æËøÓ«Èøˆ»Áœ¬±ÌÀ˘ 棨œ¬¡–Àµ∑®’˝»∑µƒ «£®°°°°£©
æËøÓ ˝∂Ó | 10 | 20 | 30 | 50 | 100 |
»À ˝ | 2 | 4 | 5 | 3 | 1 |
A. ÷⁄ ˝ «100 B. ÷–Œª ˝ «30 C. º´≤Ó «20 D. ∆Ωæ˘ ˝ «30
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com