
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是弧
是弧![]() 上一点,且
上一点,且![]() ,
,![]() 与
与![]() 交与点
交与点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,延长![]() ,
,![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长和
的长和![]() 的半径.
的半径.
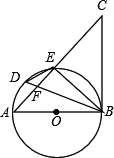
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)已知![]() ,
,![]() ,得到
,得到![]() 根据
根据![]() 是
是![]() 的直径,得到
的直径,得到![]() ,所以
,所以![]() ,即可证明
,即可证明![]() 是
是![]() 的切线.
的切线.
(2)利用同弧所对的圆周角相等和角平分线的定义可得到∠DEA=∠DBE,通过证得△DEF∽△DBE即可求解;
(3)根据题意画出图形,连接DA、DO,不难得到OD∥BE,进而有![]() ,由PA=AO可得到
,由PA=AO可得到![]() ,结合ED的长即可得到PD的长;由圆内接四边形的对角互补可得到∠ABE+∠ADE=180°,结合平角和平行线的性质可得到∠PDA=∠AOD,进一步可得到△PDA∽△POD,结合相似三角形的性质即可得到OA的长.
,结合ED的长即可得到PD的长;由圆内接四边形的对角互补可得到∠ABE+∠ADE=180°,结合平角和平行线的性质可得到∠PDA=∠AOD,进一步可得到△PDA∽△POD,结合相似三角形的性质即可得到OA的长.
(1)∵![]() ,
,![]()
∴![]()
∵![]() 是
是![]() 的直径
的直径
∴![]()
∴![]()
∴![]()
即![]()
又∵![]() 是
是![]() 的直径
的直径
∴![]() 是
是![]() 的切线
的切线
(2)∵∠DEA和∠ABD都是![]() 所对的圆周角,
所对的圆周角,
∴∠DEA=∠ABD
∵BD平分∠ABE
∴∠ABD=∠DBE
∴∠DEA=∠DBE
∵∠EDB=∠BDE,∠DEA=∠DBE,
∴△DEF∽△DBE,
∴![]()
∴![]()
(3)根据题意画出图形,连接DA、DO
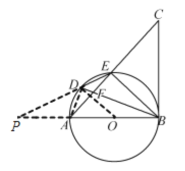
∵OD=OB,
∴∠ODB=∠OBD
∵∠EBD=∠OBD
∴∠EBD=∠ODB
∴OD∥BE
∴![]()
∵PA=AO
∴PA=AO=OB,
∴![]()
∴![]()
∴![]()
∵DE=2,
∴PD=4
∵∠PDA+∠ADE=180°,∠ABE+∠ADE=180°,
∴∠PDA=∠ABE
∵OD∥BE
∴∠AOD=∠ABE,
∴∠PDA=∠AOD
∵∠P=∠P,∠PDA=∠AOD
∴△PDA∽△POD
∴![]()
设OA=x,则PA=x,PO=2x
∵PD=4,![]() ,PA=x,PO=2x
,PA=x,PO=2x
∴![]()
∴x=![]()
∴OA=![]()
故答案为:![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,作对角线
中,作对角线![]() 的垂直平分线
的垂直平分线![]() ,垂足为点
,垂足为点![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
(2)如图2,当![]() ,且
,且![]() 时,在不添加任何辅助线情况下,请直接写出图2中的四条线段,使写出的每条线段长度都等于
时,在不添加任何辅助线情况下,请直接写出图2中的四条线段,使写出的每条线段长度都等于![]() 长度的
长度的![]() 倍.
倍.
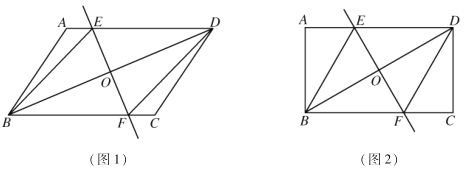
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学现有的五个社团:![]() .文学,
.文学,![]() .辩论,
.辩论,![]() .体育,
.体育,![]() .奥数,
.奥数,![]() .围棋,为了选出“你最喜爱的社团”,在部分同学中开展了调查( 每名被调查的同学必须且只能选出一个社团),并将调查结果进行了统计,绘制了如下两幅不完整的统计图:
.围棋,为了选出“你最喜爱的社团”,在部分同学中开展了调查( 每名被调查的同学必须且只能选出一个社团),并将调查结果进行了统计,绘制了如下两幅不完整的统计图:
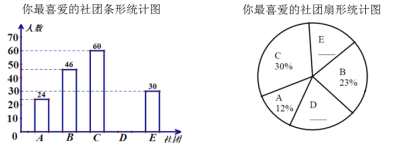
![]() 求本次被调查的人数;
求本次被调查的人数;
![]() 将上面两幅统计图补充完整;
将上面两幅统计图补充完整;
![]() 若该学校大约有学生
若该学校大约有学生![]() 人,请你估计喜欢体育社团的人数;
人,请你估计喜欢体育社团的人数;
![]() 学校为社团安排了
学校为社团安排了![]() 号教室供社团活动使用,文学设社和辩论社使用的教室恰好相邻的概率是多少?
号教室供社团活动使用,文学设社和辩论社使用的教室恰好相邻的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,可得到△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1,则△AnCnCn+1的周长为_______(n≥1,且n为整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,点B位于(4,0)、(5,0)之间,与y轴交于点C,对称轴为直线x=2,直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴上方且横坐标小于5,则下列结论:①4a+b+c>0;②a﹣b+c<0;③m(am+b)<4a+2b(其中m为任意实数);④a<﹣1,其中正确的是( )

A.①②③④B.①②③C.①②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
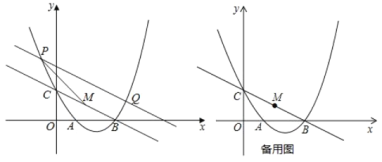
【题目】抛物线![]() 与x轴交于A、B两点,与y轴交于C,其中B(4,0),C(0,2),点P为抛物线上一动点,过点P作PQ平行BC交抛物线于Q.
与x轴交于A、B两点,与y轴交于C,其中B(4,0),C(0,2),点P为抛物线上一动点,过点P作PQ平行BC交抛物线于Q.
(1)求抛物线的解析式;
(2)①当P、Q两点重合时,PQ所在直线解析式为 ;②在①的条件下,取线段BC中点M,连接PM,判断以点P、O、M、B为顶点的四边形是什么四边形,并说明理由?
(3)已知N(0,![]() ),连接BN,K(3,0),KE∥y轴,交BN于E,x轴上有一动点F,∠EFN=60°,求OF的长.
),连接BN,K(3,0),KE∥y轴,交BN于E,x轴上有一动点F,∠EFN=60°,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某风景区内有一瀑布,AB表示瀑布的垂直高度,在与瀑布底端同一水平位置的点D处测得瀑布顶端A的仰角β为45°,沿坡度i=1:3的斜坡向上走100米,到达观景台C,在C处测得瀑布顶端A的仰角α为37°,若点B、D、E在同一水平线上.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈3.16)
≈3.16)
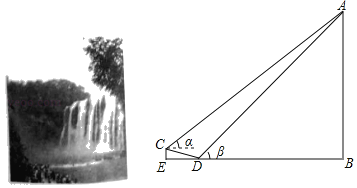
(1)观景台的高度CE为 米(结果保留准确值);
(2)求瀑布的落差AB(结果保留整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com