
【题目】某风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,小明家把一步行台阶由倾角45°改为倾角为30°,已知原台阶坡面AB的长为5m(BC所在地面为水平面),结果准确到0.1m,参考数据:![]() ,
,![]()
(1)改后的台阶坡面会加长多少?
(2)改好的台阶多占多长一段水平地面?

【答案】(1)约2.1米.(2)改善后的台阶多占2.6米长的一段水平地面.
【解析】
(1)在直角三角形ABC中利用三角函数即可求得AC、然后在直角三角形ADC中求得AD的长,AD﹣AB即是所求的解.
(2)在Rt△ABC中,由BC=ABcos45°求得BC长,再由CD=![]() 求得CD的长,根据BD=CD﹣BC可得答案.
求得CD的长,根据BD=CD﹣BC可得答案.
解:(1)∵在直角三角形ABC中,AC=ABsin45°=![]() (m)
(m)
在直角三角形ADC中,AD=![]() (米),
(米),
∴AD﹣AB=(5![]() ﹣5)(米)≈5×(1.414﹣1)=2.07≈2.1(米).
﹣5)(米)≈5×(1.414﹣1)=2.07≈2.1(米).
即改善后的台阶坡面加长约2.1米.
(2)如图,在Rt△ABC中,BC=ABcos45°=5cos45°=![]() (米).
(米).
在Rt△ACD中,CD= (米).
(米).
∴BD=CD﹣BC=![]() ≈2.6(米).
≈2.6(米).
答:改善后的台阶多占2.6米长的一段水平地面.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
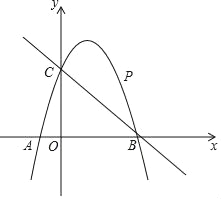
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
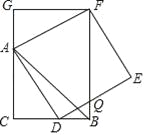
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,其中正确的结论的个数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)
(1)找出该样本数据的众数和中位数;
(2)计算这些车的平均速度;(结果精确到0.1)
(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.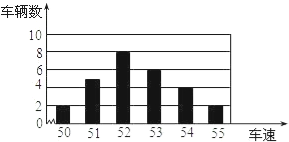
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=4,点E是AD的中点,将矩形ABCD沿直线BE折叠,点A对应点为点A',延长BA',交边DC于点F.若点F是DC的三等分点,则CD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李同学根据6位同学在一次数学测试中的成绩绘制了一条形统计图(如图).
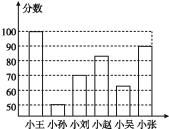
(1)哪位同学的分数最高,哪位同学的分数最低,他们相差多少?
(2)小张的分数是小孙分数的几倍?
(3)这个图易使人产生错误的感觉吗?为什么?
(4)为了更为直观、清楚地反映这6名同学的分数状况,这个图应做怎样的改动?
查看答案和解析>>
科目:初中数学 来源: 题型:
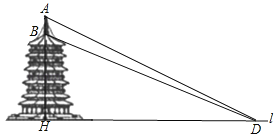
【题目】如图,一座古塔AH的高为33米,AH⊥直线l,某校九年级数学兴趣小组为了测得该古塔塔刹AB的高,在直线l上选取了点D,在D处测得点A的仰角为26.6°,测得点B的仰角为22.8°,求该古塔塔刹AB的高.(精确到0.1米)(参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.5,sin22.8°=0.39,cos22.8°=092,tan22.8°=0.42)
查看答案和解析>>
科目:初中数学 来源: 题型:
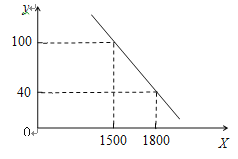
【题目】商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:
(1)请写出这种空气净化器每周的销售量y与 售价x的函数关系式(不写自变量的范围);
(2)若空气净化器每周的销售利润为W(元),则当售价为多少时,可获得最大利润,此时的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
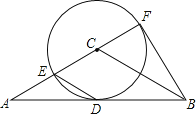
【题目】如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为点D,直线AC交⊙C于点E、F,且CF=![]() AC,
AC,
(1)求证:△ABF是直角三角形.
(2)若AC=6,则直接回答BF的长是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com