
【题目】如图,在矩形ABCD中,BC=4,点E是AD的中点,将矩形ABCD沿直线BE折叠,点A对应点为点A',延长BA',交边DC于点F.若点F是DC的三等分点,则CD的长为_____.

【答案】![]() 或2
或2![]()
【解析】
设CD=3x,分DF=x,DF=2x两种情况讨论,由折叠性质可得AB=A'B,∠BA'E=∠A=90°,AE=A'E,由“HL”可证Rt△A'EF≌Rt△DEF,可得A'F=DF,由勾股定理可求CD的长.
解:如图,连接EF
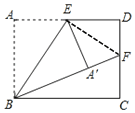
∵四边形ABCD是矩形
∴AB=CD,∠A=∠D=90°
∵点E是AD中点
∴AE=DE,
∵将矩形ABCD沿直线BE折叠,
∴AB=A'B,∠BA'E=∠A=90°,AE=A'E
∴A'E=DE,EF=EF
∴Rt△A'EF≌Rt△DEF(HL)
∴DF=A'F
设AB=CD=3x=A'B,
若DF=x,
∴A'F=x,CF=2x
∴BF=4x,
在Rt△BCF中,BF2=CF2+BC2,
∴16x2=4x2+16
∴x=![]()
∴CD=3x=2![]()
若DF=2x,则CF=x,
同理可得:CD=![]()
故答案为:![]() 或2
或2![]()


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
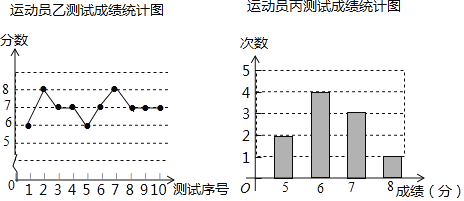
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为( )
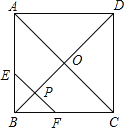
A. 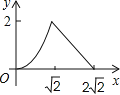 B.
B. 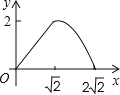
C. 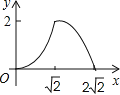 D.
D. 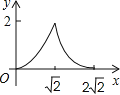
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是集体跳绳的示意图,绳子在最高处和最低处时可以近似看作两条对称的抛物线,分别记为C1和C2,绳子在最低点处时触地部分线段CD=2米,两位甩绳同学的距离AB=8米,甩绳的手最低点离地面高度AE=BN=![]()
![]() 米,最高点离地AF=BM=
米,最高点离地AF=BM=![]() 米,以地面AB、抛物线对称轴GH所在直线为x轴和y轴建立平面直角坐标系.
米,以地面AB、抛物线对称轴GH所在直线为x轴和y轴建立平面直角坐标系.
(1)求抛物线C1和C2的解析式;
(2)若小明离甩绳同学点A距离1米起跳,至少要跳多少米以上才能使脚不被绳子绊住?
(3)若集体跳绳每相邻两人(看成两个点)之间最小距离为0.8米,腾空后的人的最高点头顶与最低点脚底之距为1.5米,请通过计算说明,同时进行跳绳的人数最多可以容纳几人?(温馨提醒:所有同学起跳处均在直线CD上,不考虑错时跳起问题,即身体部分均在C1和C2之间才算通过),(参考数据:![]()
![]() =1.414,
=1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数频率 | 频数 |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
合计 | 40 | 1.00 |
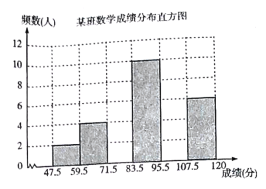
根据表中提供的信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ,
,![]() ;
;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百分比约为 ;
(3)补充完整频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,小明家把一步行台阶由倾角45°改为倾角为30°,已知原台阶坡面AB的长为5m(BC所在地面为水平面),结果准确到0.1m,参考数据:![]() ,
,![]()
(1)改后的台阶坡面会加长多少?
(2)改好的台阶多占多长一段水平地面?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某外国语学校组织九年级学生参加数学、科学、英语竞赛培训,如图两幅统计图反映了学生自愿报名(每人限报一科)的情况,请你根据图中信息回答下列问题:

(1)九年级报名参加三科培训的总人数是_____.
(2)英语学科所占扇形圆心角的度数是_____,请补全上述统计图.
(3)根据实际情况,需从英语组抽调部分同学到数学组,使数学组人数是英语组人数的3倍,则应从英语组抽调多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:
月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:![]() 书法比赛;
书法比赛;![]() 国画竞技;
国画竞技;![]() 诗歌朗诵;
诗歌朗诵;![]() 汉字大赛;
汉字大赛;![]() 古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
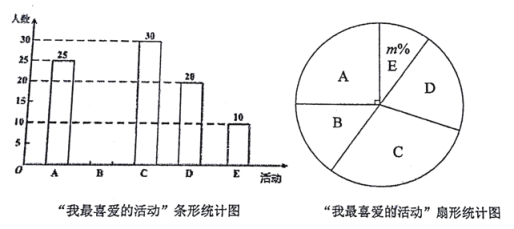
(1)此次催记抽取的初三学生共 人,![]() ,并补全条形统计图;
,并补全条形统计图;
(2)初三年级准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用树状图或列表法求选出的两名选手正好是一男一女的概率是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com