
【题目】如图是集体跳绳的示意图,绳子在最高处和最低处时可以近似看作两条对称的抛物线,分别记为C1和C2,绳子在最低点处时触地部分线段CD=2米,两位甩绳同学的距离AB=8米,甩绳的手最低点离地面高度AE=BN=![]()
![]() 米,最高点离地AF=BM=
米,最高点离地AF=BM=![]() 米,以地面AB、抛物线对称轴GH所在直线为x轴和y轴建立平面直角坐标系.
米,以地面AB、抛物线对称轴GH所在直线为x轴和y轴建立平面直角坐标系.
(1)求抛物线C1和C2的解析式;
(2)若小明离甩绳同学点A距离1米起跳,至少要跳多少米以上才能使脚不被绳子绊住?
(3)若集体跳绳每相邻两人(看成两个点)之间最小距离为0.8米,腾空后的人的最高点头顶与最低点脚底之距为1.5米,请通过计算说明,同时进行跳绳的人数最多可以容纳几人?(温馨提醒:所有同学起跳处均在直线CD上,不考虑错时跳起问题,即身体部分均在C1和C2之间才算通过),(参考数据:![]()
![]() =1.414,
=1.414,![]() ≈1.732)
≈1.732)

【答案】(1) ![]() ;(2) 至少要
;(2) 至少要![]() 跳米以上才能使脚不被绳子绊住;(3) 8人.
跳米以上才能使脚不被绳子绊住;(3) 8人.
【解析】
(1)先写出点C、D、E、F的坐标,然后设解析式代入求解即可;
(2)小明离甩绳同学点A距离1米起跳,可得此点的横坐标,代入C2解析式,即可求得;
(3)用y1减去y2,让其等于1.5,解出相应点的横坐标,求出这两个点的横坐标之间的距离,然后用间隔0.8乘以人数减1,即可解出.
解:(1)由已知得:C(﹣1,0),D(1,0),E(﹣4,![]() ),F(﹣4,
),F(﹣4,![]() ),
),
设C2解析式为:![]() ,把
,把![]() 代入得15a=
代入得15a=![]() ,
,
∴![]() ,
,
∴![]() .
.
由对称性,设C1解析式![]() ,把F(﹣4,
,把F(﹣4,![]() )代入得c=
)代入得c=![]() ,
,
∴![]()
故答案为:抛物线C1和C2的解析式分别为:![]() ,
,![]() .
.
(2)把x=﹣3代入![]() 得
得![]() ,
,
∴至少要跳![]() 米以上才能使脚不被绳子绊住.
米以上才能使脚不被绳子绊住.
(3)由y1﹣y2=1.5得:![]()
∴![]() ,
,
∴x1﹣x2=![]() ≈4×1.414=5.656,
≈4×1.414=5.656,
设同时进行跳绳的人数最多可以容纳x人
则0.8(x﹣1)≤5.656,
∴x≤8.07
∴同时进行跳绳的人数最多可以容纳8人.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
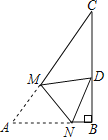
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
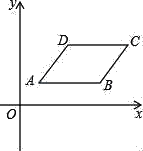
【题目】如图,在平面直角坐标系中,ABCD的边AB=2,顶点A坐标为(1,b),点D坐标为(2,b+1)
(1)点B的坐标是 ,点C的坐标是 (用b表示);
(2)若双曲线y=![]() 过ABCD的顶点B和D,求该双曲线的表达式;
过ABCD的顶点B和D,求该双曲线的表达式;
(3)若ABCD与双曲线y=![]() (x>0)总有公共点,求b的取值范围.
(x>0)总有公共点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
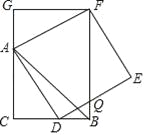
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,其中正确的结论的个数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)
(1)找出该样本数据的众数和中位数;
(2)计算这些车的平均速度;(结果精确到0.1)
(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.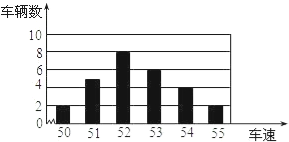
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=4,点E是AD的中点,将矩形ABCD沿直线BE折叠,点A对应点为点A',延长BA',交边DC于点F.若点F是DC的三等分点,则CD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
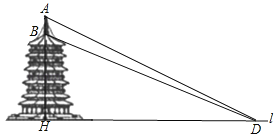
【题目】如图,一座古塔AH的高为33米,AH⊥直线l,某校九年级数学兴趣小组为了测得该古塔塔刹AB的高,在直线l上选取了点D,在D处测得点A的仰角为26.6°,测得点B的仰角为22.8°,求该古塔塔刹AB的高.(精确到0.1米)(参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.5,sin22.8°=0.39,cos22.8°=092,tan22.8°=0.42)
查看答案和解析>>
科目:初中数学 来源: 题型:
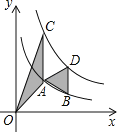
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com