
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
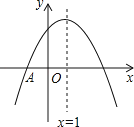
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
利用抛物线开口方向得到a<0,再由抛物线的对称轴方程得到b=﹣2a,则3a+b=a,于是可对①进行判断;利用2≤c≤3和c=﹣3a可对②进行判断;利用二次函数的性质可对③进行判断;根据抛物线y=ax2+bx+c与直线y=n﹣1有两个交点可对④进行判断.
解:∵抛物线开口向下,
∴a<0,
而抛物线的对称轴为直线x=﹣![]() =1,即b=﹣2a,
=1,即b=﹣2a,
∴3a+b=3a﹣2a=a<0,所以①正确;
∵2≤c≤3,
而c=﹣3a,
∴2≤﹣3a≤3,
∴﹣1≤a≤﹣![]() ,所以②正确;
,所以②正确;
∵抛物线的顶点坐标(1,n),
∴x=1时,二次函数值有最大值n,
∴a+b+c≥am2+bm+c,
即a+b≥am2+bm,所以③正确;
∵抛物线的顶点坐标(1,n),
∴抛物线y=ax2+bx+c与直线y=n﹣1有两个交点,
∴关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.
故选:D.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图;
(3)若该中学约有2400名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)
(1)找出该样本数据的众数和中位数;
(2)计算这些车的平均速度;(结果精确到0.1)
(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.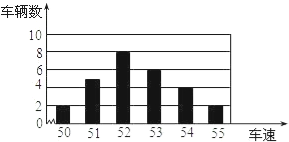
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李同学根据6位同学在一次数学测试中的成绩绘制了一条形统计图(如图).
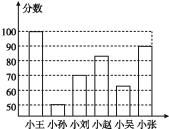
(1)哪位同学的分数最高,哪位同学的分数最低,他们相差多少?
(2)小张的分数是小孙分数的几倍?
(3)这个图易使人产生错误的感觉吗?为什么?
(4)为了更为直观、清楚地反映这6名同学的分数状况,这个图应做怎样的改动?
查看答案和解析>>
科目:初中数学 来源: 题型:
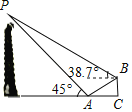
【题目】河南省开封市铁塔始建于公元1049年(北宋皇祐元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明在铁塔一侧的水平面上一个台阶的底部A处测得塔顶P的仰角为45°,走到台阶顶部B处,又测得塔顶P的仰角为38.7°,已知台阶的总高度BC为3米,总长度AC为10米,试求铁塔的高度.(结果精确到1米,参考数据:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下面四个命题,其中真命题的个数有( )
(1)平分弦的直径垂直于这条弦,并且平分这条弦所对的弧;
(2)90°的圆周角所对的弦是直径;
(3)在同圆或等圆中,圆心角的度数是圆周角的度数的两倍;
(4)如下图,顺次连接圆的任意两条直径的端点,所得的四边形一定是矩形.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com