
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图;
(3)若该中学约有2400名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.

【答案】(1)这次被调查的学生有50人;(2)m=0.2,n=10,p=20,补图见解析;(3)估计全校学生中利用手机购物或玩游戏的共有1200人,建议见解析.
【解析】
(1)利用“总数=频数÷百分比”直接进行计算即可
(2)利用“频数=总数×百分比,百分比=频数÷总数”直接进行计算即可
(3)用2400乘以手机购物或玩游戏的总百分比即可
(1)从C可看出5÷0.1=50人,
答:这次被调查的学生有50人;
(2)m=![]() =0.2,n=0.2×50=10,p=0.4×50=20,
=0.2,n=0.2×50=10,p=0.4×50=20,
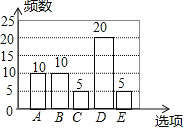
(3) 2400×(0.1+0.4)=2400×0.5=1200人,
答:全校学生中利用手机购物或玩游戏的共有1200人,可利用手机学习.


科目:初中数学 来源: 题型:
【题目】某校计划在暑假第二周的星期一至星期四开展社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择两天,其中有一天是星期二的概率是多少?
(2)乙同学随机选择连续的两天,其中有一天是星期二的概率是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均为整数),则有
均为整数),则有![]() .
.
![]() ,
,![]() .这样小明就找到了一种把类似
.这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当![]() 、
、![]() 、
、![]() 、
、![]() 均为正整数时,若
均为正整数时,若![]() ,用含
,用含![]() 、
、![]() 的式子分别表示
的式子分别表示![]() 、
、![]() ,得:
,得:![]() ,
,![]() ;
;
(2)利用所探索的结论,找一组正整数![]() 、
、![]() 、
、![]() 、
、![]() 填空:
填空: ![]()
![]()
![]()
![]()
![]() ;
;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均为正整数,求
均为正整数,求![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角![]() 内接于⊙O,
内接于⊙O, ![]() 于点D,连结AO.
于点D,连结AO.
⑴若![]() .
.
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
⑵点E在线段OA上,![]() ,连接DE,设
,连接DE,设![]() ,
,![]() (m、n是正数),若
(m、n是正数),若![]() ,求证:
,求证:![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
(1)(探索发现)
在△ABC中,AC=BC,∠ACB=a,点D为直线BC上一动点(点D不与点B,C重合),过点D作DF∥AC交直线AB于点F,将AD绕点D顺时针旋转a得到ED,连接BE,如图(1),当点D在线段BC上,且a=90°时,试猜想:
①AF与BE之间的数量关系: ;
②∠ABE= .
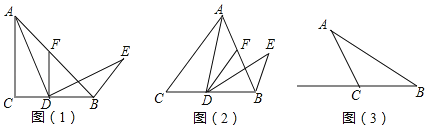
(2)(拓展探究)
如图(2),当点D在线段BC上,且0°<a<90°时,判断AF与BE之间的数量关系及∠ABE的度数,请说明理由.
(3)(解决问题)
如图(3),在△ABC中,AC=BC,AB=4,∠ACB=a,点D在射线BC上,将AD绕点D顺时针旋转a得到ED,连接BE.当BD=3CD时,请直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)请你添加一个适当的条件 ,使得四边形ABCD是平行四边形,并证明你的结论;
(2)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(3)在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=![]() ,求⊙O的半径.
,求⊙O的半径.
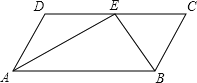
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当四边形MENF是正方形时,求AD:AB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
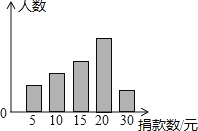
【题目】某学生会倡导的“爱心捐款”活动结束后,学生会干部对捐款情况作了抽样调查,并绘制了统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
(1)他们一共抽查了多少人?
(2)这组数据的众数、中位数分别是多少?
(3)若该校共有2310名学生,请估算有多少人捐款数不少于20元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
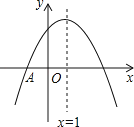
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com