
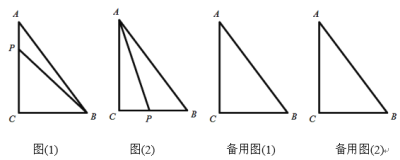
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点P从点A开始沿着
,若动点P从点A开始沿着![]() 的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
(1)当![]() 时,
时,![]() 的面积是___________
的面积是___________![]() ;
;
(2)如图(2)当t为何值时,AP平分![]() ;
;
(3)当t为何值时,![]() 为等腰三角形.
为等腰三角形.
【答案】(1)45;(2)![]() ;(3)t=2.5秒或25或26.5或23.75.
;(3)t=2.5秒或25或26.5或23.75.
【解析】
(1)当t=3时,求出AP的长,再根据三角形面积公式即可得出结果;
(2)作PD⊥AB于D,由勾股定理求出AB的长,由角平分线性质得出PD=PC=2t-20(cm),AD=AC=20cm,求出BD的长,得出PB=BC-PC=35-2t(cm),在Rt△PBD中,由勾股定理求出t的值即可;
(3)由于点P是动点,故应分点P在AC上与AB上两种情况进行讨论,根据等腰三角形的性质和相似三角形的判定与性质即可得出结果.
(1)当t=3时,AP=2×3=6(cm),
△ABP的面积=![]() AP×BC=
AP×BC=![]() ×6×15=45(cm2);
×6×15=45(cm2);
故答案为:45cm2;
(2)作PD⊥AB于D,如图2所示:
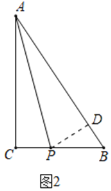
∵在△ABC中,∠C=90°,AC=20cm,BC=15cm,
∴AB=![]() (cm),
(cm),
∵AP平分∠CAB,
∴PD=PC=2t-20(cm),AD=AC=20cm,
∴BD=AB-AD=5cm,
∴PB=BC-PC=15-(2t-20)=35-2t(cm),
在Rt△PBD中,由勾股定理得:BD2+PD2=PB2,
即52+(2t-20)2=(35-2t)2,
解得:t=![]() ,
,
∴当t为![]() 时,AP平分∠CAB;
时,AP平分∠CAB;
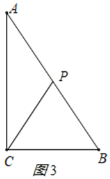
(3)当点P在AC上时,CP=CB=15cm,
∴AP=AC-CP=5cm,
∴t=2.5秒;
当点P在AB上时,分三种情况:
若BP=BC=15cm,t=(20+15+15)÷2=25(秒);
若CP=BC=15cm,
作CM⊥AB,则BM=PM,
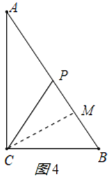
∵∠B=∠B,∠BMC=∠BCA,
∴△ABC∽△CBM,
∴![]() ,即
,即![]() ,
,
解得:CM=12cm,BM=9cm,
∴PB=2BM=18cm,
∴t=(20+15+18)÷2=26.5(秒);
若PC=PB,则∠B=∠BCP,
∵∠B+∠A=90°,∠BCP+∠ACP=90°,
∴∠A=∠ACP,
∴AP=CP=BP=![]() AB=12.5cm,
AB=12.5cm,
∴t=(20+15+12.5)÷2=23.75(秒);
综上所述,当t=2.5秒或25或26.5或23.75秒时,△BCP为等腰三角形.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】在自习课上,小明拿来如下框的一道题目(原问题)和合作学习小组的同学们交流.
如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F.探究线段DF与EF的数量关系.
小红同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小华同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
请你参考小明同学的思路,探究并解决以下问题:
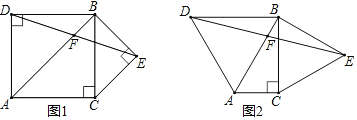
(1)写出原问题中DF与EF的数量关系为 .
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是AC的中点,直角
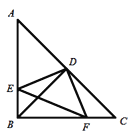
,点D是AC的中点,直角![]() 的两边分别交AB、BC于点E、F,给出以下结论:①
的两边分别交AB、BC于点E、F,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 是等腰直角三角形. 当
是等腰直角三角形. 当![]() 在
在![]() 内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点
路径向终点![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点
路径向终点![]() 以
以![]() 的速度运动,两点都要到达相应的终点时才能停止运动.分别过
的速度运动,两点都要到达相应的终点时才能停止运动.分别过![]() 和
和![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,则当运动时间
,则当运动时间![]() ____________
____________![]() 时,
时,![]() 与去
与去![]() 全等.
全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC中,A、B、C的坐标分别为A(﹣1,2),B(﹣3,﹣2),C(1,﹣1),将△ABC向上平移3个单位,再向右平移2个单位.

(1)作出平移后的△A1B1C1,并写出A1,B1,C1的坐标.
(2)求△A1B1C1的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com