
 如图,在平行四边形ABCD中,AB=5,AD=2,∠B=60°,以点B为圆心,BC为半径的圆弧交AB于点E,连接DE,则图中阴影部分的面积为$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π.(结果保留π)
如图,在平行四边形ABCD中,AB=5,AD=2,∠B=60°,以点B为圆心,BC为半径的圆弧交AB于点E,连接DE,则图中阴影部分的面积为$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π.(结果保留π) 分析 过点C作CF⊥BA,易求平行四边形ABCD、扇形CBE、△DAE的面积,利用阴影部分的面积=平行四边形的面积-扇形面积-△DAE面积计算即可.
解答 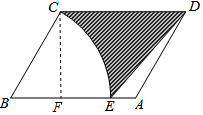 解:过点A作AF⊥BC,
解:过点A作AF⊥BC,
∵BC=AD=2,∠B=60°,
∴CF=$\sqrt{3}$,
∴平行四边形ABCD面积=AB•CF=5$\sqrt{3}$,
∴扇形ABE面积=$\frac{60π×{2}^{2}}{360}$=$\frac{2}{3}$π,
∵AD=BC=2,BE=2,
∴AE=3,
∴△DAE的面积=$\frac{1}{2}$AE•CF=$\frac{3}{2}$$\sqrt{3}$,
∴阴影部分的面积=平行四边形的面积-扇形面积-△DAE面积=5$\sqrt{3}$-$\frac{2}{3}$π-$\frac{3}{2}$$\sqrt{3}$=$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π,
故答案为:$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π.
点评 本题考查了平行四边形的性质、扇形的面积公式运用、三角形面积公式运用,解题的关键是作平行四边形的高线,构造直角三角形,并且求出其高线的长度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$$\sqrt{2}$ | B. | -$\frac{7}{2}$$\sqrt{2}$ | C. | $\frac{9}{\sqrt{2}}$ | D. | -$\frac{7}{\sqrt{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
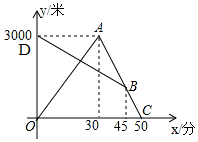 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
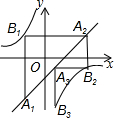 如图,已知:n为正整数,点A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直线y=x-1上,点B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为-1,则点A2017的坐标为( )
如图,已知:n为正整数,点A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直线y=x-1上,点B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为-1,则点A2017的坐标为( )| A. | (-1,-2) | B. | (2,1) | C. | ($\frac{1}{2}$,$-\frac{1}{2}$) | D. | ($\frac{1}{2}$,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com