
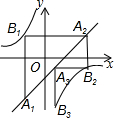
 如图,已知:n为正整数,点A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直线y=x-1上,点B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为-1,则点A2017的坐标为( )
如图,已知:n为正整数,点A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直线y=x-1上,点B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为-1,则点A2017的坐标为( )| A. | (-1,-2) | B. | (2,1) | C. | ($\frac{1}{2}$,$-\frac{1}{2}$) | D. | ($\frac{1}{2}$,-2) |
分析 ①先求点A1的坐标;
②根据A1B1⊥x轴时,A1、B1的横坐标相等,求B1的坐标;
③根据B1A2⊥y轴时,B1、A2的纵坐标相等,求A2的坐标;
同理可求A3、A4的坐标并发现规律,计算2017与3的商,得出结论.
解答 解:当x=-1时,y=-1-1=-2,
∴A1(-1,-2),
当A1B1⊥x轴时,y=-$\frac{1}{-1}$=1,
∴B1(-1,1),
当B1A2⊥y轴,当y=1时,x-1=1,x=2,
∴A2(2,1),
当A2B2⊥x轴,当x=2时,y=-$\frac{1}{2}$,
∴B2(2,-$\frac{1}{2}$),
当B2A3⊥y轴,当y=-$\frac{1}{2}$时,-$\frac{1}{2}$=x-1,x=$\frac{1}{2}$,
∴A3($\frac{1}{2}$,-$\frac{1}{2}$),
当A3B3⊥x轴时,当x=$\frac{1}{2}$时,y=-$\frac{1}{\frac{1}{2}}$=-2,
∴B3($\frac{1}{2}$,-2),
当B3A4⊥y轴时,y=-2,x-1=-2,x=-1,
∴A4(-1,-2),
…
发现,点A1,A2,A3,A4…An的坐标每三个一循环,
2017÷3=672…余1,
∴则点A2017的坐标为(-1,-2);
故选A.
点评 本题考查了反比例和一次函数的交点问题以及点的坐标的规律,明确垂直于x轴的直线上的点的纵坐标相等,垂直于y轴的直线上的点的横坐标相等得出各点的坐标,使问题得以解决.


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,AB=5,AD=2,∠B=60°,以点B为圆心,BC为半径的圆弧交AB于点E,连接DE,则图中阴影部分的面积为$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π.(结果保留π)
如图,在平行四边形ABCD中,AB=5,AD=2,∠B=60°,以点B为圆心,BC为半径的圆弧交AB于点E,连接DE,则图中阴影部分的面积为$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
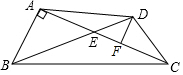 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,DF∥AB,交AC于F,∠DCE=30°,AB=DC=5,BC=13,求AC的长和四边形ABCD的面积.
如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,DF∥AB,交AC于F,∠DCE=30°,AB=DC=5,BC=13,求AC的长和四边形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,根据图形填空
如图,根据图形填空查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com