练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．在△ABC中，AD是∠BAC的平分线，若∠B=50°，∠C=70°，则∠CAD的度数是（　　）
    A．15°B．30°C．60°D．120°

    分析 利用三角形的内角和先求∠BAC的度数，再运用角平分线的定义，求∠CAD的度数即可．

    解答 解：∵∠B=50°，∠C=70°，
    ∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°．
    ∵AD是∠BAC的平分线，
    ∴∠CAD=$\frac{1}{2}$∠BAC=30°．
    故选：B．

    点评 本题主要考查了三角形的内角和和外角的性质的综合运用，注意角平分线的正确运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

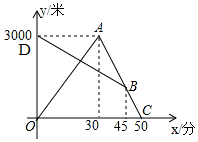    14．某天早晨，张强从家跑步去体育锻炼，同时妈妈从体育场晨练结束回家，途中两人相遇，张强跑到体育场后发现要下雨，立即按原路返回，遇到妈妈后两人一起回到家（张强和妈妈始终在同一条笔直的公路上行走）．如图是两人离家的距离y（米）与张强出发的时间x（分）之间的函数图象，根据图象信息解答下列问题：
    （1）求张强返回时的速度为150米/分，点B的坐标为（45，750）；
    （2）分别求线段BD和AC的函数解析式；
    （3）请直接写出张强与妈妈何时相距1000米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知S1=x，S2=3S1-2，S3=3S2-2，S4=3S3-2，…，S2017=3S2016-2，则S3用含x的代数式表示为S3=9x-8；S2017=32016x-32016+1．（结果用含x的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：
    （1）$\sqrt{20}$+$\sqrt{125}$；
    （2）（$\sqrt{48}$+$\sqrt{20}$）+（ $\sqrt{12}$-$\sqrt{5}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．若关于字母x的多项式-5x2-2mx2+2x-1+x2-3nx+5不含二次项和一次项，求m、n值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知三角形三个内角的度数之比为2：2：5，则其最大内角的度数是   100°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

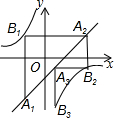    16．如图，已知：n为正整数，点A1（x1，y1），A2（x2，y2），A3（x3，y3），A4（x4，y4）…An（xn，yn）均在直线y=x-1上，点B1（m1，p1），B2（m2，p2），B3（m3，p3）…Bn（mn，pn）均在双曲线y=-$\frac{1}{x}$上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，A3B3⊥x轴，…，AnBn⊥x轴，BnAn+1⊥y轴，若点A1的横坐标为-1，则点A2017的坐标为（　　）
    A．（-1，-2）B．（2，1）C．（$\frac{1}{2}$，$-\frac{1}{2}$）D．（$\frac{1}{2}$，-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知|ab|=-ab，|b|=b，且ab≠0，|a|＞|b|
    （1）填空：a＜0，b＞0，a-b＜0，a+b＜0
    （2）化简：2|a|-|b|+3|a-b|-|a+b|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如果关于x的一元二次方程k2x2+2（k-1）x+1=0有两个不相等的实数根．
    （1）求k的取值范围；
    （2）若方程的一个实数根是1，求k的值．

    查看答案和解析>>

    同步练习册答案