
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式![]() 成立的一对有理数
成立的一对有理数![]() 为“理想有理数对”,记为
为“理想有理数对”,记为![]() ,如:数对
,如:数对![]() 、
、![]() 都是“理想有理数对”.
都是“理想有理数对”.
(1)数对![]() 、
、![]() 中是“理想有理数对”的是______;
中是“理想有理数对”的是______;
(2)若![]() 是“理想有理数对”,求a的值;
是“理想有理数对”,求a的值;
(3)若![]() 是“理想有理数对”,则
是“理想有理数对”,则![]() ______“理想有理数对”(填“是”、“不是”或“不确定”);
______“理想有理数对”(填“是”、“不是”或“不确定”);
(4)请再写出一对符合条件的“理想有理数对”.(不能与题目中已有的数对重复).
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】已知,![]() 、
、![]() 在数轴上对应的数分别用
在数轴上对应的数分别用![]() 、
、![]() 表示,且
表示,且![]() .
.
![]()
(1)数轴上点![]() 表示的数是________,点
表示的数是________,点![]() 表示的数是___________;
表示的数是___________;
(2)若一动点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位长度秒速度由
个单位长度秒速度由![]() 向
向![]() 运动;动点
运动;动点![]() 从原点
从原点![]() 出发,以
出发,以![]() 个单位长度
个单位长度![]() 秒速度向
秒速度向![]() 运动,点
运动,点![]() 、
、![]() 同时出发,点
同时出发,点![]() 运动到
运动到![]() 点时两点同时停止.设点
点时两点同时停止.设点![]() 运动时间为
运动时间为![]() 秒.
秒.
①若![]() 从
从![]() 到
到![]() 运动,则
运动,则![]() 点表示的数为_______,
点表示的数为_______,![]() 点表示的数为___________(用含
点表示的数为___________(用含![]() 的式子表示)
的式子表示)
②当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
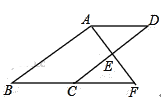
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB⊥AF,BC=12,EF=6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每个小正方形的边长都是单位1,直线a与直线b交于点O,△ABC的顶点均在格点上.
(1)△ABC向右平移 个单位长度到△A1B1C1位置;
(2)对△ABC分别作下列变换:
① 画出△ABC关于直线a对称的△A2B2C2;
② 将△ABC绕点O旋转180°,画出旋转后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中,
① △ 与△ 成轴对称,对称轴是直线 ;
② △ 与△ 成中心对称,并在图中标出对称中心D的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=3cm,PN=4cm,MN=4.5cm,则线段QR的长为( )
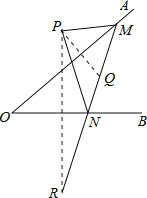
A.4.5 B.5.5 C.6.5 D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
材料1:对称,也许是中国人最喜欢的。建筑师梁思成曾说过:“无论东方、西方,再没有一个民族对中轴对称线如此钟爱与恪守。”放眼中国的建筑,无论是宫殿、庙宇、亭台、楼阁、园林无不有着对称之美。数学世界也里有一些正整数你无论从左往右看,还是从右往左看,数字都是完全一样的,例如:11、101、2332、1234321、…,像这样的数我们叫它“对称数”.
材料2:如果一个三位数![]() ,满足a+b+c=8,我们就称这个三位数为“发财数”.
,满足a+b+c=8,我们就称这个三位数为“发财数”.
(1)请直接写出既是“对称数”又是“发财数”的所有三位数;
(2)一个三位“对称数”十位数字为7,它的各数位上的数字之和是一个自然数的平方,求这个三位数(请写出必要的推理过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①![]() ,②
,②![]() ,③
,③![]() 三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.

(1)这三个命题中,真命题的个数为________;
(2)选择一个真命题,并且证明.(要求写出每一步的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com