
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
【答案】(1) 7+![]() ;(2) t为3s、5.4s、6s、6.5s;(3) t为2或6秒.
;(2) t为3s、5.4s、6s、6.5s;(3) t为2或6秒.
【解析】
(1)根据速度为每秒1cm,求出出发2秒后CP的长,然后就知AP的长,利用勾股定理求得PB的长,最后即可求得周长.
(2)因为AB与CB,由勾股定理得AC=4 因为AB为5cm,所以必须使AC=CB,或CB=AB,所以必须使AC或AB等于3,有两种情况,△BCP为等腰三角形.
(3)分类讨论:当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,t+2t-3=6;当P点在AB上,Q在AC上,则AC=t-4,AQ=2t-8,t-4+2t-8=6.
解:(1)如图1,由∠C=90°,AB=5cm,BC=3cm,
∴AC=4,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴出发2秒后,则CP=2,
∵∠C=90°,
∴PB=![]() =
=![]() ,
,
∴△ABP的周长为:AP+PB+AB=2+5+![]() =7+
=7+![]() .
.
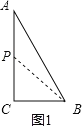
(2)①如图2,若P在边AC上时,BC=CP=3cm,
此时用的时间为3s,△BCP为等腰三角形;
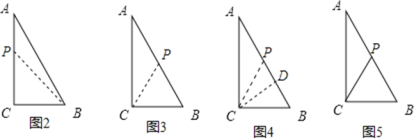
②若P在AB边上时,有三种情况:
i)如图3,若使BP=CB=3cm,此时AP=2cm,P运动的路程为2+4=6cm,
所以用的时间为6s,△BCP为等腰三角形;
ii)如图4,若CP=BC=3cm,过C作斜边AB的高,根据面积法求得高为2.4cm,
作CD⊥AB于点D,
在Rt△PCD中,PD=![]() =1.8,
=1.8,
所以BP=2PD=3.6cm,
所以P运动的路程为9-3.6=5.4cm,
则用的时间为5.4s,△BCP为等腰三角形;
ⅲ)如图5,若BP=CP,此时P应该为斜边AB的中点,P运动的路程为4+2.5=6.5cm
则所用的时间为6.5s,△BCP为等腰三角形;
综上所述,当t为3s、5.4s、6s、6.5s时,△BCP为等腰三角形
(3)如图6,当P点在AC上,Q在AB上,则PC=t,BQ=2t-3,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t+2t-3=3,
∴t=2;
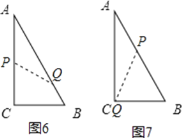
如图7,当P点在AB上,Q在AC上,则AP=t-4,AQ=2t-8,
∵直线PQ把△ABC的周长分成相等的两部分,
∴t-4+2t-8=6,
∴t=6,
∴当t为2或6秒时,直线PQ把△ABC的周长分成相等的两部分.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】将正整数![]() 至
至![]() 按照一定规律排成下表:
按照一定规律排成下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…… |
记![]() 表示第
表示第![]() 行第
行第![]() 个数,如
个数,如![]() 表示第
表示第![]() 行第
行第![]() 个数是
个数是![]() .
.
(1)直接写出![]() _______________,
_______________,![]() _______________;
_______________;
(2)①如果![]() ,那么
,那么![]() _________________,
_________________,![]() ________;②用
________;②用![]() ,
,![]() 表示
表示![]() __________;
__________;
(3)将表格中的![]() 个阴影格子看成一个整体并平移,所覆盖的
个阴影格子看成一个整体并平移,所覆盖的![]() 个数之和能否等于
个数之和能否等于![]() .若能,求出这
.若能,求出这![]() 个数中的最小数,若不能说明理由.
个数中的最小数,若不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干等长的木棒按如图的方式摆放.
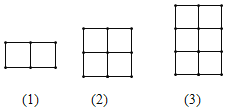
![]() 填写下表:
填写下表:
图形编号 |
|
|
|
|
|
|
木棒根数 | 7 | 12 | ______ | ______ | ______ |
|
![]() 搭第n个图形需要多少根木棒?
搭第n个图形需要多少根木棒?
![]() 搭第几个图形需要2017根木棒?
搭第几个图形需要2017根木棒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式![]() 成立的一对有理数
成立的一对有理数![]() 为“理想有理数对”,记为
为“理想有理数对”,记为![]() ,如:数对
,如:数对![]() 、
、![]() 都是“理想有理数对”.
都是“理想有理数对”.
(1)数对![]() 、
、![]() 中是“理想有理数对”的是______;
中是“理想有理数对”的是______;
(2)若![]() 是“理想有理数对”,求a的值;
是“理想有理数对”,求a的值;
(3)若![]() 是“理想有理数对”,则
是“理想有理数对”,则![]() ______“理想有理数对”(填“是”、“不是”或“不确定”);
______“理想有理数对”(填“是”、“不是”或“不确定”);
(4)请再写出一对符合条件的“理想有理数对”.(不能与题目中已有的数对重复).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过A(2,0),B(0,-6)两点.
的图象经过A(2,0),B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
(3)在x轴上是否存在一点P,使△ABP为等腰三角形,若存在,求出P的坐标,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面给出的数轴,解答下面的问题:
![]()
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: ,B: ;
(2)观察数轴,与点A的距离为4的点表示的数是: ;
(3)若将数轴折叠,使得A点与﹣3表示的点重合,则B点与数 表示的点重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东56°,射线 OC在∠NOE内,且∠NOC与∠BOS互余,射线OA平分∠BON,图中与∠COA互余的角是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别从
,甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向而行.已知甲车速度为
两地同时出发,相向而行.已知甲车速度为![]() ,乙车速度为
,乙车速度为![]() ,经过
,经过![]() 后两车相距
后两车相距![]() ,则
,则![]() 的值是( )
的值是( )
A.2B.10C.2或10D.2或2.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com