
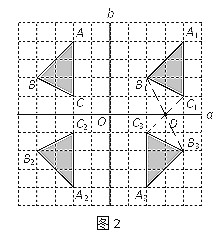
【题目】在如图的正方形网格中,每个小正方形的边长都是单位1,直线a与直线b交于点O,△ABC的顶点均在格点上.
(1)△ABC向右平移 个单位长度到△A1B1C1位置;
(2)对△ABC分别作下列变换:
① 画出△ABC关于直线a对称的△A2B2C2;
② 将△ABC绕点O旋转180°,画出旋转后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中,
① △ 与△ 成轴对称,对称轴是直线 ;
② △ 与△ 成中心对称,并在图中标出对称中心D的位置.

【答案】(1)6;(2)①详见解析;②详见解析;(3)① A2B2C2,A3B3C3,b;② A1B1C1,A3B3C3,点D的位置详见解析.
【解析】
(1)根据直角坐标系的特点即可得到△ABC向右平移6个单位长度到△A1B1C1;
(2)①找到△ABC各顶点关于直线a的对称点,再顺次连接即可;
②找到△ABC各顶点关于O点的对称点,再顺次连接即可
(3)①根据轴对称的性质即可判断;②根据中心对称的性质即可判断,连接对应点的连接,交点即为对称中心D的位置.
(1)△ABC向右平移6个单位长度到△A1B1C1位置
故答案为:6;
(2)如图2,①A2B2C2为所求,②A3B3C3为所求;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中,
① △A2B2C2与△A3B3C3成轴对称,对称轴是直线b;
② △A1B1C1与△A3B3C3成中心对称,如图,D为所求
故答案为:① A2B2C2,A3B3C3,b; ② A1B1C1,A3B3C3,


科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,线段AC=8cm,BC=4cm,点M、N分别是AC、BC的中点, 求:
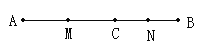
(1) 线段MN的长度.
(2) 根据(1)的计算过程和结果,设AC+BC=![]() ,其它条件不变,你能猜测出MN的长度吗?请证明你的猜测.
,其它条件不变,你能猜测出MN的长度吗?请证明你的猜测.
查看答案和解析>>
科目:初中数学 来源: 题型:
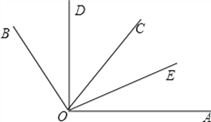
【题目】如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,AD∥BC,过B作BE⊥AD交AD于点E,AB=13cm,BC=21cm,AE=5cm.动点P从点C出发,在线段CB上以每秒1cm的速度向点B运动,动点Q同时从点A出发,在线段AD上以每秒2cm的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动,设运动的时间为t(秒)
(1)当t为何值时,四边形PCDQ是平行四边形?
(2)当t为何值时,△QDP的面积为60cm2?
(3)当t为何值时,PD=PQ?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干等长的木棒按如图的方式摆放.
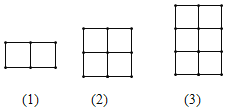
![]() 填写下表:
填写下表:
图形编号 |
|
|
|
|
|
|
木棒根数 | 7 | 12 | ______ | ______ | ______ |
|
![]() 搭第n个图形需要多少根木棒?
搭第n个图形需要多少根木棒?
![]() 搭第几个图形需要2017根木棒?
搭第几个图形需要2017根木棒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】幂的运算:
(1)计算:(﹣a3)2+(﹣a2)3
(2)计算:![]()
(3)![]()
(4)我们已经学习了四个关于幂的运算法则:①aman=am+n;②(am)n=amn;③(ab)m=ambm;④am÷an=am﹣n,下面是小明计算的过程(a3a2)3=(a3+2)3=(a5)3=a15,他用到的公式有 (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式![]() 成立的一对有理数
成立的一对有理数![]() 为“理想有理数对”,记为
为“理想有理数对”,记为![]() ,如:数对
,如:数对![]() 、
、![]() 都是“理想有理数对”.
都是“理想有理数对”.
(1)数对![]() 、
、![]() 中是“理想有理数对”的是______;
中是“理想有理数对”的是______;
(2)若![]() 是“理想有理数对”,求a的值;
是“理想有理数对”,求a的值;
(3)若![]() 是“理想有理数对”,则
是“理想有理数对”,则![]() ______“理想有理数对”(填“是”、“不是”或“不确定”);
______“理想有理数对”(填“是”、“不是”或“不确定”);
(4)请再写出一对符合条件的“理想有理数对”.(不能与题目中已有的数对重复).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面给出的数轴,解答下面的问题:
![]()
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: ,B: ;
(2)观察数轴,与点A的距离为4的点表示的数是: ;
(3)若将数轴折叠,使得A点与﹣3表示的点重合,则B点与数 表示的点重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com