
【题目】已知:在⊙O中,弦AC⊥弦BD,垂足为H,连接BC,过点D作DE⊥BC于点E,DE交AC于点F.
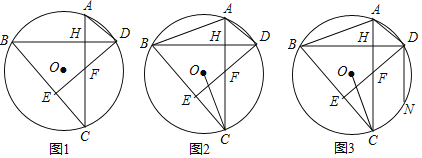
(1)如图1,求证:BD平分∠ADF;
(2)如图2,连接OC,若AC=BC,求证:OC平分∠ACB;
(3)如图3,在(2)的条件下,连接AB,过点D作DN∥AC交⊙O于点N,若AB=3![]() ,DN=9.求sin∠ADB的值.
,DN=9.求sin∠ADB的值.
【答案】(1)证明见解析;(2)证明见解析;(3)sin∠ADB的值为![]() .
.
【解析】
(1)根据等角的余角相等即可证明;
(2)连接OA、OB.只要证明△OCB≌△OCA即可解决问题;
(3)如图3中,连接BN,过点O作OP⊥BD于点P,过点O作OQ⊥AC于点Q,则四边形OPHQ是矩形,可知BN是直径,则HQ=OP=![]() DN=
DN=![]() ,设AH=x,则AQ=x+
,设AH=x,则AQ=x+![]() ,AC=2AQ=2x+9,BC=2x+9,CH=AC﹣AH=2x+9﹣x=x+9,在Rt△AHB中,BH2=AB2﹣AH2=(
,AC=2AQ=2x+9,BC=2x+9,CH=AC﹣AH=2x+9﹣x=x+9,在Rt△AHB中,BH2=AB2﹣AH2=(![]() )2﹣x2.在Rt△BCH中,BC2=BH2+CH2即(2x+9)2=(
)2﹣x2.在Rt△BCH中,BC2=BH2+CH2即(2x+9)2=(![]() )2﹣x2+(x+9)2,解得 x=3,BC=2x+9=15,CH=x+9=12求出sinBCH,即为sin∠ADB的值.
)2﹣x2+(x+9)2,解得 x=3,BC=2x+9=15,CH=x+9=12求出sinBCH,即为sin∠ADB的值.
(1)证明:如图1,
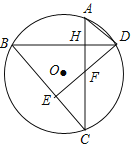
∵AC⊥BD,DE⊥BC,
∴∠AHD=∠BED=90°,
∴∠DAH+∠ADH=90°,∠DBE+∠BDE=90°,
∵∠DAC=∠DBC,
∴∠ADH=∠BDE,
∴BD平分∠ADF;
(2)证明:连接OA、OB.
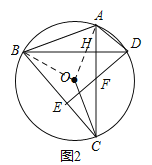
∵OB=OC=OA,AC=BC,
∴△OCB≌△OCA(SSS),
∴∠OCB=∠OCA,
∴OC平分∠ACB;
(3)如图3中,连接BN,过点O作OP⊥BD于点P,过点O作OQ⊥AC于点Q.

则四边形OPHQ是矩形,
∵DN∥AC,
∴∠BDN=∠BHC=90°,
∴BN是直径,
则OP=![]() DN=
DN=![]() ,
,
∴HQ=OP=![]() ,
,
设AH=x,则AQ=x+![]() ,AC=2AQ=2x+9,BC=AC=2x+9,
,AC=2AQ=2x+9,BC=AC=2x+9,
∴CH=AC﹣AH=2x+9﹣x=x+9
在Rt△AHB中,BH2=AB2﹣AH2=(![]() )2﹣x2.
)2﹣x2.
在Rt△BCH中,BC2=BH2+CH2,
即(2x+9)2=(![]() )2﹣x2+(x+9)2,
)2﹣x2+(x+9)2,
整理得2x2+9x﹣45=0,
(x﹣3)(2x+15)=0,
解得: x=3(负值舍去),
BC=2x+9=15,CH=x+9=12
∵∠ADB=∠BCH,
∴sin∠ADB=sin∠BCH=![]() =
=![]() =
=![]() .
.
即sin∠ADB的值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.
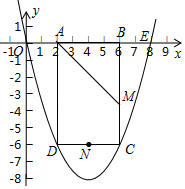
(1)求抛物线的解析式;
(2)F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;
(3)在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为![]() ?若存在,求出点P的坐标;若不存在,请说明理由;
?若存在,求出点P的坐标;若不存在,请说明理由;
(4)矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
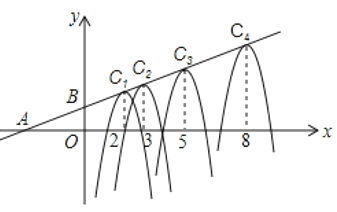
,![]() ,形状相同的抛物线
,形状相同的抛物线![]() 的顶点在直线
的顶点在直线![]() 上,其对称轴与
上,其对称轴与![]() 轴的交点的横坐标依次为2,3,5,18,13,…,根据上述规律,抛物线
轴的交点的横坐标依次为2,3,5,18,13,…,根据上述规律,抛物线![]() 的顶点坐标为_________.
的顶点坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
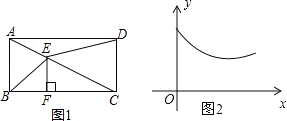
A.线段BEB.线段EFC.线段CED.线段DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:(一)如果两个函数y1,y2,存在x取同一个值,使得y1=y2,那么称y1,y2为“合作函数”,称对应x的值为y1,y2的“合作点”;
(二)如果两个函数为y1,y2为“合作函数”,那么y1+y2的最大值称为y1,y2的“共赢值”.
(1)判断函数y=x+2m与y=![]() 是否为“合作函数”,如果是,请求出m=1时它们的合作点;如果不是,请说明理由;
是否为“合作函数”,如果是,请求出m=1时它们的合作点;如果不是,请说明理由;
(2)判断函数y=x+2m与y=3x﹣1(|x|≤2)是否为“合作函数”,如果是,请求出合作点;如果不是,请说明理由;
(3)已知函数y=x+2m与y=x2﹣(2m+1)x+(m2+4m﹣3)(0≤x≤5)是“合作函数”,且有唯一合作点.
①求出m的取值范围;
②若它们的“共赢值”为24,试求出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com