练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】矩形ABCD中，AB=10，AD=4，点P是CD上的动点，当∠APB=90°时，DP的长是（ ）

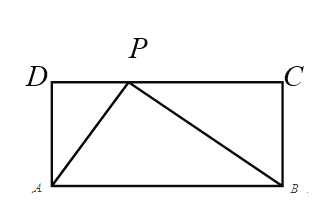
    A.2B.6C.2或6D.2或8

    【答案】D

    【解析】

    以AB的中点O为圆心，AB的一半5为半径作圆，交CD于点P，点P即为所求；设PC＝x，则PD＝10﹣x，证△ADP∽△PCB得，即，解之可得答案．

    解：如图，以AB的中点O为圆心，AB的一半5为半径作圆，交CD于点P，点P即为所求；

    设PC＝x，则PD＝10﹣x，

    ∵四边形ABCD是矩形，

    ∴∠D＝∠C＝90°，

    ∴∠DAP+∠APD＝90°，

    ∵∠APB＝90°，

    ∴∠APD+∠BPC＝90°，

    ∴∠DAP＝∠CPB，

    ∴△ADP∽△PCB，

    ∴，即，

    解得：x＝2或8，

    PD＝10﹣x＝2或8，即PD＝2或8．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

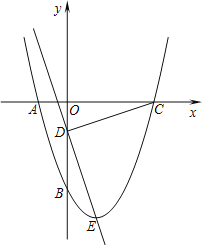
    【题目】如图所示，抛物线y=x2+bx+c经过A、B两点，A、B两点的坐标分别为（﹣1，0）、（0，﹣3）．

    （1）求抛物线的函数解析式；

    （2）点E为抛物线的顶点，点C为抛物线与x轴的另一交点，点D为y轴上一点，且DC=DE，求出点D的坐标；

    （3）在第二问的条件下，在直线DE上存在点P，使得以C、D、P为顶点的三角形与△DOC相似，请你直接写出所有满足条件的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高学生书写汉字的能力，增强保护汉字的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为（分），且，将其按分数段分为五组，绘制出以下不完整表格：

    组别

    成绩（分）

    频数（人数）

    频率

    一

    2

    0.04

    二

    10

    0.2

    三

    14

    b

    四

    a

    0.32

    五

    8

    0.16

    请根据表格提供的信息，解答以下问题：

    （1）本次决赛共有________名学生参加；

    （2）直接写出表中_________，_________；

    （3）请补全下面相应的频数分布直方图；

    （4）若决赛成绩不低于80分为优秀，则本次大赛的优秀率为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y＝ax2＋bx＋c(a≠0)的图象经过点A，B，C．现有下面四个推断：①抛物线开口向下；②当x=－2时，y取最大值；③当m<4时，关于x的一元二次方程ax2＋bx＋c=m必有两个不相等的实数根；④直线y=kx+c(k≠0)经过点A，C，当kx+c> ax2＋bx＋c时，x的取值范围是－4<x<0；其中推断正确的是 （ ）

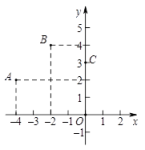
    A. ①②B. ①③C. ①③④D. ②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的对角线相交于点O，点E，F分别是边BC上两点，且.将绕点O逆时针旋转，当点F与点C重合时，停止旋转.已知，BC=6，设BE=x，EF=y.

    小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.

    下面是小明的探究过程，请补充完整：

    (1)按照下表中自变量x的值进行取点、画图、测量，得到了y与x的几组对应值；

    x

    0

    0.5

    1

    1.5

    2

    2.5

    3

    y

    3

    2.77

    2.50

    2.55

    2.65

    (说明：补全表格时相关数值保留一位小数)

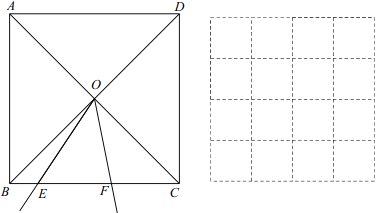
    (2)建立平面直角坐标系，描出补全后的表中各对对应值为坐标的点，画出该函数的图象；

    (3)结合函数图象，解决问题：当EF=2BE时，BE的长度约为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

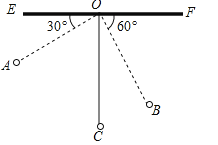
    【题目】（2017内蒙古通辽市）如图，物理教师为同学们演示单摆运动，单摆左右摆动中，在OA的位置时俯角∠EOA=30°，在OB的位置时俯角∠FOB=60°，若OC⊥EF，点A比点B高7cm．求：

    （1）单摆的长度（≈1.7）；

    （2）从点A摆动到点B经过的路径长（π≈3.1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣5，1），B（﹣2，2），C（﹣1，4），请按下列要求画图：

    （1）将△ABC先向右平移4个单位长度、再向下平移1个单位长度，得到△A1B1C1，画出△A1B1C1；

    （2）画出与△ABC关于原点O成中心对称的△A2B2C2，并直接写出点A2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在⊙O中，弦AC⊥弦BD，垂足为H，连接BC，过点D作DE⊥BC于点E，DE交AC于点F．

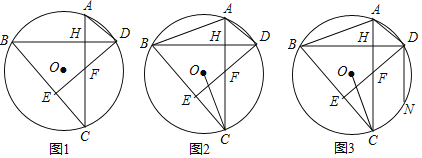
    （1）如图1，求证：BD平分∠ADF；

    （2）如图2，连接OC，若AC＝BC，求证：OC平分∠ACB；

    （3）如图3，在（2）的条件下，连接AB，过点D作DN∥AC交⊙O于点N，若AB＝3，DN＝9．求sin∠ADB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门，2019也被称为中国科幻片的元年．某电影院为了全面了解观众对《流浪地球》的满意度情况，进行随机抽样调查，分为四个类别：A．非常满意；B．满意；C．基本满意；D．不满意．依据调查数据绘制成图1和图2的统计图（不完整）．根据以上信息，解答下列问题：

    （1）本次接受调查的观众共有　 　人；

    （2）扇形统计图中，扇形C的圆心角度数是　 　．

    （3）请补全条形统计图；

    （4）春节期间，该电影院来观看《流浪地球》的观众约3000人，请估计观众中对该电影满意（A、B、C类视为满意）的人数．

    查看答案和解析>>

    同步练习册答案