
分析 根据比例的性质,可得ab=cd,根据完全平方公式,可得a2d2+b2c2=abcd+abcd,根据等式的性质,可得a2b2+a2d2+b2c2+c2d2=a2b2+abcd+abcd+c2d2,根据因式分解,可得(a2+c2)(b2+d2)=(ab+cd)(ab+cd),根据等式的性质,可得答案.
解答 证明:∵$\frac{a}{b}$=$\frac{c}{d}$,
∴ad=bc.即ad-bc=0,
∴(ad-bc)2=0.
∴a2d2+b2c2=abcd+abcd.
a2b2+a2d2+b2c2+c2d2=a2b2+abcd+abcd+c2d2,
∴(a2+c2)(b2+d2)=(ab+cd)(ab+cd)
$\frac{{a}^{2}+{c}^{2}}{ab+cd}$=$\frac{ab+cd}{{b}^{2}+{d}^{2}}$.
点评 本题考查了比例的性质,利用完全平方公式得出a2d2+b2c2=abcd+abcd,再利用因式分解得出(a2+c2)(b2+d2)=(ab+cd)(ab+cd)是解题关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
 2014年,山西省某地实施了“免费校车工程”.小明原来骑自行车上学,现在乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.已知小明家距学校5千米,若校车速度是他骑车速度的2倍,设小明骑车的速度为x千米/小时,则所列方程正确的为( )
2014年,山西省某地实施了“免费校车工程”.小明原来骑自行车上学,现在乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.已知小明家距学校5千米,若校车速度是他骑车速度的2倍,设小明骑车的速度为x千米/小时,则所列方程正确的为( )| A. | $\frac{5}{x}$+$\frac{1}{6}$=$\frac{5}{2x}$ | B. | $\frac{5}{x}$=$\frac{5}{2x}$+$\frac{1}{6}$ | C. | $\frac{5}{x}$+10=$\frac{5}{2x}$ | D. | $\frac{5}{x}$-10=$\frac{5}{2x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
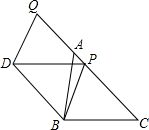 如图,在△ABC中,AB=8,sin∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为6.
如图,在△ABC中,AB=8,sin∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com