
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QO,设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )
A.
B.
C.
D.
【答案】D
【解析】解:∵∠ABE=45°,∠A=90°,
∴△ABE是等腰直角三角形,
∴AE=AB=2,BE= ![]() AB=2
AB=2 ![]() ,
,
∵BE=DE,PD=x,
∴PE=DE﹣PD=2 ![]() ﹣x,
﹣x,
∵PQ∥BD,BE=DE,
∴QE=PE=2 ![]() ﹣x,
﹣x,
又∵△ABE是等腰直角三角形(已证),
∴点Q到AD的距离= ![]() (2
(2 ![]() ﹣x)=2﹣
﹣x)=2﹣ ![]() x,
x,
∴△PQD的面积y= ![]() x(2﹣
x(2﹣ ![]() x)=﹣
x)=﹣ ![]() (x2﹣2
(x2﹣2 ![]() x+2)=﹣
x+2)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
即y=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]()
纵观各选项,只有C选项符合.
故答案为:D.
先得出△ABE是等腰直角三角形,进而求出AE、BE的长,表示出PE、QE,从而求出点Q到AD的距离,由三角形的面积公式可得到y与x的关系式,根据解析式可判断出图象.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:初中数学 来源: 题型:
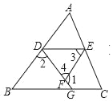
【题目】如图,已知∠1+∠2=180°,∠3=∠B,试判断DE与BC的位置关系,并对结论进行说理.
证明:DE∥BC.
理由如下:
∵∠1+∠2=180°(已知)
∠1+∠4=180°(平角定义)
∴∠2=∠4(同角的补角相等)
∴ ∥ ( )
∴∠3+ =180°( )
∵∠3=∠B(已知)
∴∠B+ =180°(等量代换)
∴ ∥ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
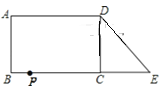
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知![]() ,
,![]() 交
交![]() 于
于![]() ,那么图1中
,那么图1中![]() 、
、![]() 、
、![]() 之间有什么数量关系?并说明理由.
之间有什么数量关系?并说明理由.
(2)如图2,已知![]() ,点
,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,
,![]() 和
和![]() 的平分线交于点
的平分线交于点![]() ,请利用(1)的结论求图2中
,请利用(1)的结论求图2中![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D.
(1)求证:PB是⊙O的切线.
(2)当BC=2 ![]() ,cos∠AOD=
,cos∠AOD= ![]() 时,求PB的长.
时,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
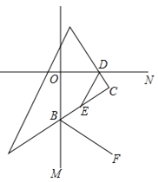
【题目】如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
(1)填空:∠OBC+∠ODC= ;
(2)如图,若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3∶4∶5∶8∶6,又知此次调查中捐款25元和30元的学生一共42人.

(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=10a×10b,例如图3*4=103×104=107.
(1)试求12*3和2*5的值;
(2)想一想(a*b)*c与a*(b*c)相等吗?如果相等,请验证你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com