
【题目】我们规定:a*b=10a×10b,例如图3*4=103×104=107.
(1)试求12*3和2*5的值;
(2)想一想(a*b)*c与a*(b*c)相等吗?如果相等,请验证你的结论.
【答案】(1)1015,107;(2)不一定相等.
【解析】
(1)根据题目所给的运算法则求解.
(2)根据题目所给的运算法则分别计算左右两边,看看结果是不是相等即可判定.
(1)解:12*3=1012×103=1015 , 2*5=102×105=107
(2)解:不一定相等.
∵(a*b)*c=(10a×10b)*c=10a+b*c=![]() ×10c=
×10c=![]() ,
,
a*(b*c)=a*(10b×10c)=a*10b+c=10a×![]() =
=![]() ,
,
当a≠c时,(a*b)*c≠a*(b*c),
当a=c时,(a*b)*c=a*(b*c),
综上所述,(a*b)*c与a*(b*c)不一定相等.
∴(a*b)*c≠a*(b*c)


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QO,设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.

查看答案和解析>>
科目:初中数学 来源: 题型:
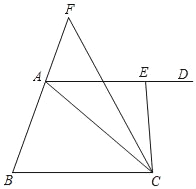
【题目】如图,在△ABC中,∠CAB=∠CBA,过点A向右作AD∥BC,点E是射线AD上的一个动点,∠ACE的平分线交BA的延长线于点F.
(1)若∠ACB=40°,∠ACE=38°,求∠F的度数;
(2)在动点E运动的过程中,![]() 的值是否发生变化?若不变,求它的值;若变化,请说明理由.
的值是否发生变化?若不变,求它的值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设京西绿色走廊,改善永定河水质,某治污公司决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格与月处理污水量如下表:

经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求x、y的值;
(2)如果治污公司购买污水处理设备的资金不超过105万元,求该治污公司有哪几种购买方案;
(3)在(2)的条件下,如果月处理污水量不低于2040吨,为了节约资金,请为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
问题情境:如图1,在△ABC中,AB=AC,点D,E分别是边AB,AC上的点,且AD=AE,连接DE,易知BD=CE.将△ADE绕点A顺时针旋转角度α(0°<α<360°),连接BD,CE,得到图2.
(1)变式探究:如图2,若0°<α<90°,则BD=CE的结论还成立吗?若成立,请证明;若不成立,请说明理由;
(2)拓展延伸:若图1中的∠BAC=120°,其余条件不变,请解答下列问题:
从A,B两题中任选一题作答我选择 题
A.①在图1中,若AB=10,求BC的长;
②如图3,在△ADE绕点A顺时针旋转的过程中,当DE的延长线经过点C时,请直接写出线段AD,BD,CD之间的等量关系;
B.①在图1中,试探究BC与AB的数量关系,并说明理由;
②在△ADE绕点A顺时针旋转的过程中,当点D,E,C三点在同一条直线上时,请借助备用图探究线段AD,BD,CD之间的等量关系,并直接写出结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
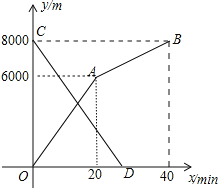
【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用![]() 小亮骑自行车以
小亮骑自行车以![]() 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程![]() 与各自离开出发地的时间
与各自离开出发地的时间![]() 之间的函数图象如图所示,
之间的函数图象如图所示,
![]() 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______![]() ;
;
![]() 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
![]() 求两人相遇的时间.
求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
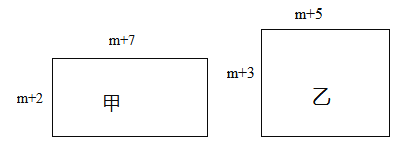
【题目】已知有甲、乙两个长方形,它们的边长如图所示(m为正整数),面积分别为S1、S2.
(1)请比较S1与S2的大小: S1 S2;
(2)若一个正方形与甲的周长相等.
①求该正方形的边长(用含m的代数式表示);
②若该正方形的面积为S3,试探究:S3与S1的差(即S3﹣S1)是否为常数?若为常数,求出这个常数;如果不是,请说明理由;
(3)若满足条件0<n<|S1﹣S2|的整数n有且只有8个,直接写出m的值并分别求出S1与S2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com