
【题目】如图所示,抛物线y=ax2+bx+3与x轴交于点A、B两点(A在B的左侧)与y轴交于C点,且OA:OC=1:3,S△ABC=6.

(1)求抛物线的函数关系式;
(2)抛物线上是否存在一点D(点C除外),使S△ABD=S△ABC?若存在,求出D点坐标;若不存在,说明理由.
(3)抛物线上是否存在一点E(点B除外),使S△ACE=S△ABC?若存在,求出E点坐标;若不存在,说明理由.
【答案】(1)y=﹣x2+2x+3;(2)抛物线上存在一点D(点C除外),使S△ABD=S△ABC,D点坐标(2,3),(1﹣![]() ,﹣3),D(1+
,﹣3),D(1+![]() ,﹣3);(3)存在,E(﹣4.﹣21).
,﹣3);(3)存在,E(﹣4.﹣21).
【解析】
试题分析:(1)根据三角形的面积,可得AB的长,根据线段的和差,可得B点坐标,根据待定系数法,可得函数解析式;
(2)根据平行线间的距离相等,可得D点的纵坐标,根据函数值,可得答案;
(3)根据平行线的一次函数的一次项系数相等,可得BE的解析式,根据解方程组,可得E点坐标.
解:(1)当x=0时,y=3,即OC=3.
由OA:OC=1:3,
解得OA=1,即A点坐标为(﹣1,0).
由S△ABC=![]() ABOC=6,
ABOC=6,
解得AB=4.﹣1+4=3,
即B(3,0).
将A、B点的坐标代入函数解析式,得![]() ,
,
解得![]() ,
,
抛物线的解析式为y=﹣x2+2x+3;
(2)如图1:
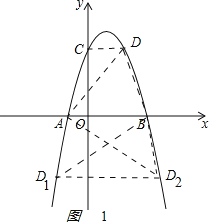 ,
,
根据平行线间的距离相等,可得D点的纵坐标为3或﹣3.
当y=3时,﹣x2+2x+3=3,解得x=0(不符合题意,舍),x=2,
即D点的坐标为(2,3);
当y=﹣3时,﹣x2+2x+3=﹣3.
解得x=1﹣![]() ,x=1+
,x=1+![]() ,
,
即D点坐标为(1﹣![]() ,﹣3),(1+
,﹣3),(1+![]() ,﹣3);
,﹣3);
综上所述:抛物线上存在一点D(点C除外),使S△ABD=S△ABC,D点坐标(2,3),(1﹣![]() ,﹣3),D(1+
,﹣3),D(1+![]() ,﹣3);
,﹣3);
(3)过点B作AC平行线,如图2
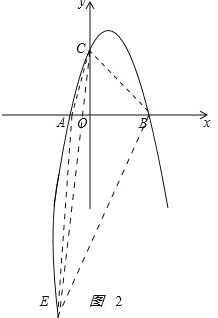 ,
,
S△ACE=S△ABC,由平行线间的距离相等,得
设AC的函数解析式y=kx+b,将A、C点的坐标代入函数解析式,得
![]() ,
,
解得![]()
函数解析式为y=3x+3,
由BE∥AC,设BE的解析式为y=3x+b,将B点坐标代入函数解析式,得
3×3+b=0.
解得b=﹣9,
即BE的解析式为y=3x﹣9,
联立BE与抛物线,得
![]() ,
,
解得x=﹣4,x=3(不符合题意,舍),
当x=﹣4时,y=3×(﹣4)﹣9=﹣21,
即E(﹣4.﹣21).


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:①AB∥CD;②ED⊥CD;③∠DFC=∠ADC﹣∠DCE;④S△EDF=S△BCF,其中正确的结论是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
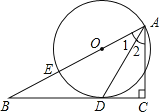
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若|a|=5,|b|=4,且点M(a,b)在第二象限,则点M的坐标是( )
A. (5,4) B. (-5,4) C. (-5,-4) D. (5,-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【课本引申】
我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
【尝试探究】
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
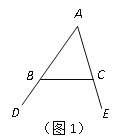
【拓展运用】
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=_________;
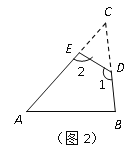
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案_ .
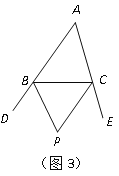
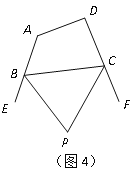
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com