
����Ŀ�����α����
����֪���������ε�һ����ǵ������������ڵ������ڽǵĺͣ���ô�������ε�һ���ڽ����������ڵ�������ǵĺ�֮�����������������ϵ�أ�
������̽����
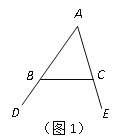
��1����ͼ1����DBC���ECB�ֱ�Ϊ��ABC��������ǣ���̽����A���DBC����ECB֮�����������������ϵ��Ϊʲô��
����չ���á�
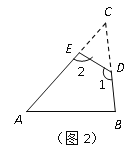
��2����ͼ2���ڡ�ABCֽƬ�м�ȥ��CED���õ��ı���ABDE������1+��2��230�㣬������ġ�C��_________��
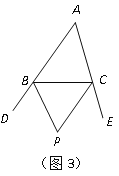
��3��С�����뵽�����������һ�����⣺��ͼ3���ڡ�ABC�У�BP��CP�ֱ�ƽ����ǡ�DBC����ECB����P���A�к�������ϵ����ֱ��д����_ ��
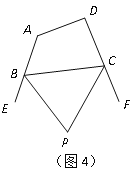
��4����ͼ4�����ı���ABCD�У�BP��CP�ֱ�ƽ����ǡ�EBC����FCB����P���A����D�к�������ϵ��Ϊʲô��(����Ҫ��������Ľ���˵������ֱ��ʹ�ã�����˵������)
���𰸡���1����DBC+��ECB =180��+��A ��2��50�㣨3����P=90�㣭![]() ��A ��4����BAD+��CDA=360�㣭2��P��
��A ��4����BAD+��CDA=360�㣭2��P��
�������������������1�����������ε�һ����ǵ������������ڵ������ڽǵĺͱ�ʾ����DBC+��ECB���������������ڽǺͶ����������ɵý⣻
��2�����ݣ�1���Ľ����������㼴�ɵý⣻
��3����ʾ����DBC+��ECB���ٸ��ݽ�ƽ���ߵĶ��������PBC+��PCB��Ȼ�������������ڽǺͶ�����ʽ�������ɵý⣻
��4���ӳ�BA��CD�ཻ�ڵ�Q�����á�Q��ʾ����P�����ã�1���Ľ����������ɵý⣻
���������
��1����DBC+��ECB=180������ABC+180������ACB
=360����(��ABC+��ACB)
=360����(180������A)
=180��+��A
��2��50��
��3����P=90����![]() ��A
��A
��4���ӳ�BA��CD���ڵ�Q��
����P=90����![]() ��Q�����Q=180����2��P��
��Q�����Q=180����2��P��
���BAD+��CDA=180��+��Q=180��+180����2��P=360����2��P��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������y=ax2+bx+3��x�ύ�ڵ�A��B���㣨A��B����ࣩ��y�ύ��C�㣬��OA��OC=1��3��S��ABC=6��

��1���������ߵĺ�����ϵʽ��
��2�����������Ƿ����һ��D����C���⣩��ʹS��ABD=S��ABC�������ڣ����D�����ꣻ�������ڣ�˵�����ɣ�
��3�����������Ƿ����һ��E����B���⣩��ʹS��ACE=S��ABC�������ڣ����E�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��|![]() ��2|+20090������
��2|+20090������![]() ����1+3tan30��
����1+3tan30��
��2���ⲻ��ʽ�飺![]()
�ⷽ�̣�
��3��x2+4x+1=0
��4��![]() =
=![]() ��1��
��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪ���η���ax2+bx+c=0��һ��Ϊ0�������н�����ȷ���ǣ� ��
A.a=0
B.b=0
C.c=0
D.c��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
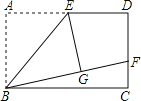
����Ŀ����ͼ������ABCD�У�E��AD���е㣬����ABE��ֱ��BE�۵���õ���GBE���ӳ�BG��CD�ڵ�F����AB=6��BC=10����FD�ij�Ϊ�� ��
A��![]() B��4 C��
B��4 C��![]() D��5
D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ�ĸ����У� ��
��һ�����������ķ�����������ķ�����ͬ��
��������������0������������
�����һ���������������������������һ����0��
��������Ϊ�෴�����������������õĽ����Ȼ��Ϊ�෴����
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У�ȥ������ȷ������ ��
A. m+(-n+x-y)=m+n+x-y B. m-(-n+x-y)=m+n+x+y
C. a-2(b+c)=a-2b+c D. a-2(b-c)=a-2b+2c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ݣ�7,a,8,b,10,c,6��ƽ������4.
(1)��a��b��c��ƽ������
(2)��2a��1,2b��1,2c��1��ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ε�һ����ǵ���40�������������εı�����( )
A. 6 B. 9 C. 12 D. 15
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com