
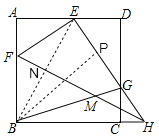
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=![]() ,AE=8,则S四边形EFMG=________.
,AE=8,则S四边形EFMG=________.

【答案】![]()
【解析】解:过B作BP⊥EH于P,连接BE,交FH于N,则∠BPG=90°,∵四边形ABCD是正方形,∴∠BCD=∠ABC=∠BAD=90°,AB=BC,∴∠BCD=∠BPG=90°,∵∠EGB=∠CGB,BG=BG,∴△BPG≌△BCG,∴∠PBG=∠CBG,BP=BC,∴AB=BP,∵∠BAE=∠BPE=90°,BE=BE,∴Rt△ABE≌Rt△PBE(HL),∴∠ABE=∠PBE,∴∠EBG=∠EBP+∠GBP=![]() ∠ABC=45°,由折叠得:BF=EF,BH=EH,∴FH垂直平分BE,∴△BNM是等腰直角三角形,∵BM=
∠ABC=45°,由折叠得:BF=EF,BH=EH,∴FH垂直平分BE,∴△BNM是等腰直角三角形,∵BM=![]() ,∴BN=NM=
,∴BN=NM=![]() =
=![]() ,∴BE=
,∴BE=![]() ,∵AE=8,∴DE=12﹣8=4,由勾股定理得:AB=
,∵AE=8,∴DE=12﹣8=4,由勾股定理得:AB=![]() =
=![]() =12,设BF=x,则EF=x,AF=12﹣x,由勾股定理得:x2=82+(12﹣x)2,x=
=12,设BF=x,则EF=x,AF=12﹣x,由勾股定理得:x2=82+(12﹣x)2,x=![]() ,∴BF=EF=
,∴BF=EF=![]() ,∵△ABE≌△PBE,∴EP=AE=8,BP=AB=12,同理可得:PG=
,∵△ABE≌△PBE,∴EP=AE=8,BP=AB=12,同理可得:PG=![]() ,Rt△EFN中,FN=
,Rt△EFN中,FN=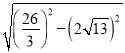 =
=![]() ,∴S四边形EFMG=S△EFN+S△EBG﹣S△BNM=
,∴S四边形EFMG=S△EFN+S△EBG﹣S△BNM=![]() FNEN+
FNEN+![]() EGBP﹣
EGBP﹣![]() BNNM=
BNNM=![]() ×
×![]() ×
×![]() +
+![]() (8+
(8+![]() )×12﹣
)×12﹣![]() ×
×![]() ×
×![]() =
=![]() .故答案为:
.故答案为: ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,学校内有一块四边形的空地ABCD,现计划在该空地上种植草坪经测量,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草坪皮需要400元,问需要投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县政府打算用25000元用于为某乡福利院购买每台价格为2000元的彩电和每台价格为1800元的冰箱,并计划恰好全部用完此款.
(1)问原计划所购买的彩电和冰箱各多少台?
(2)由于国家出台“家电下乡”惠农政策,该县政府购买的彩电和冰箱可获得13%的财政补贴,若在不增加县政府实际负担的情况下,能否多购买两台冰箱?谈谈你的想法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,a是
,a是![]() 的立方根,方程
的立方根,方程![]() 是关于x,y的二元一次方程,d为不等式组
是关于x,y的二元一次方程,d为不等式组![]() 的最大整数解.
的最大整数解.
![]() 求点A、B、C的坐标;
求点A、B、C的坐标;
![]() 如图1,若D为y轴负半轴上的一个动点,当
如图1,若D为y轴负半轴上的一个动点,当![]() 时,
时,![]() 与
与![]() 的平分线交于M点,求
的平分线交于M点,求![]() 的度数;
的度数;
![]() 如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使![]() ?若存在,请求出D的纵坐标
?若存在,请求出D的纵坐标![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
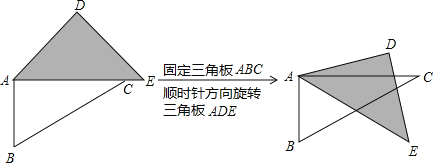
【题目】如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).当△ADE的一边与△ABC的某一边平行(不共线)时,写出旋转角α的所有可能的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少万元?
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数![]() (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 ![]() 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0;
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
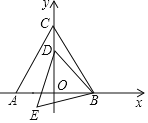
【题目】如图,△ABC是等边三角形,点A(-3,0),点B(3,0),点D是y轴上的一个动点,连接BD,将线段BD绕点B逆时针旋转60°,得到线段BE,连接DE,得到△BDE,则OE的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线CM上任意一点,在射线CM上载取CE=BD,连接AD、AE.
(1)如图1,当点D落在线段BC的延长线上时,求证:△ABD≌△ACE;
(2)在(1)的条件下,求出∠ADE的度数;
(3)如图2,当点D落在线段BC(不含端点)上时,作AH⊥BC,垂足为H,作AG⊥EC,垂足为G,连接HG,判断△GHC的形状,并说明现由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com