【题目】某县政府打算用25000元用于为某乡福利院购买每台价格为2000元的彩电和每台价格为1800元的冰箱，并计划恰好全部用完此款．
（1）问原计划所购买的彩电和冰箱各多少台？
（2）由于国家出台“家电下乡”惠农政策，该县政府购买的彩电和冰箱可获得13%的财政补贴，若在不增加县政府实际负担的情况下，能否多购买两台冰箱？谈谈你的想法．
【答案】解：（1）设原计划购买彩电
台，冰箱
台，根据题意，得
化简得：
由于
均为正整数，解得
（2）该批家电可获财政补贴为
由于多买的冰箱也可获得13%的财政补贴，实际负担为总价的87%．
∴可多买两台冰箱．
答：（1）原计划购买彩电8台和冰箱5台；
（2）能多购买两台冰箱．我的想法：可以拿财政补贴款3250元，再借350元，先购买两台冰箱回来，再从总价3600元冰箱的财政补贴468元中拿出350元用于归还借款，这样不会增加实际负担．
【解析】（1）应先找出等量关系列出方程求解．本题的等量关系为“计划恰好全部用完此款”．
（2）“县政府购买的彩电和冰箱可获得13%的财政补贴，若在不增加县政府实际负担的情况下”为此题的等量关系，列方程求解．
科目：初中数学 来源： 题型：
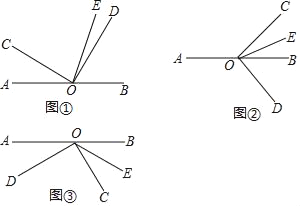
【题目】如图①，O是直线AB上的一点，∠COD是直角，OE平分∠BOC．
（1）若∠AOC=30°时，则∠DOE的度数为_____；
（2）将图①中的∠COD绕顶点O顺时针旋转至图②的位置，其它条件不变，探究∠AOC和∠DOE的度数之间的关系，写出你的结论，并说明理由；
（3）将图①中的∠COD绕顶点O顺时针旋转至图③的位置，其他条件不变．直接写出∠AOC和∠DOE的度数之间的关系：_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】中国“一带一路”战略给沿线国家和地区带来很大的经济效益，沿线某地区居民2015年年收入200美元，预计2017年年收入将达到1000美元，设2015年到2017年该地区居民年人均收入平均增长率为x，可列方程为（ ）
A. 200（1+2x）＝1000B. 200+2x＝1000
C. 200（1+x2）＝1000D. 200（1+x）2＝1000
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图1，抛物线y=﹣
x2﹣
x+3与x轴交于A和B两点（点A在点B的左侧），与y轴相交于点C，点D的坐标是（0，﹣1），连接BC、AC
（1）求出直线AD的解析式；
（2）如图2，若在直线AC上方的抛物线上有一点F，当△ADF的面积最大时，有一线段MN=
（点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF，请求出四边形AMNF的周长最小时点N的横坐标；
（3）如图3，将△DBC绕点D逆时针旋转α°（0＜α°＜180°），记旋转中的△DBC为△DB′C′，若直线B′C′与直线AC交于点P，直线B′C′与直线DC交于点Q，当△CPQ是等腰三角形时，求CP的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处；
（1）求证：B′E=BF；
（2）设AE=a，AB=b，BF=C，试猜想a，b，c之间的一种关系，并给予证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：在矩形ABCD中，AD=60cm，CD=120cm，E、F为AB边的三等分点，以EF为边在矩形内作等边三角形MEF，N为AB边上一点，EN=10cm；
请在矩形内找一点P，使△PMN为等边三角形（画出图形，并直接写出△PMF的面积）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点 
是双曲线 
在第三象限分支上的一个动点，连接 
并延长交另一分支于点 
，以 
为边作等边三角形 
，点 
在第四象限内，且随着点 
的运动，点 
的位置也在不断变化，但点 
始终在双曲线 
上运动，则 
的值是_______________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
