
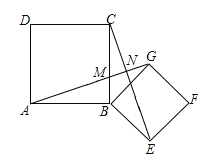
【题目】如图,四边形ABCD,四边形BEFG均为正方形,连接AG,CE.试说明:
(1)AG=CE;
(2)AG⊥CE.

【答案】(1)答案见解析;(2)答案见解析
【解析】试题分析:(1)由正方形的性质有AB=CB,∠ABC=∠GBE=90°,BG=BE,进而得出∠ABG=∠CBE,由SAS证明△ABG≌△CBE,得出对应边相等即可;
(2)由△ABG≌△CBE,得出对应角相等∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.
试题解析:证明:(1)∵四边形ABCD、BEFG均为正方形,∴AB=CB,∠ABC=∠GBE=90°,BG=BE,∴∠ABG=∠CBE.
在△ABG和△CBE中,∵AB=CB,∠ABG=∠CBE,BG=BE,∴△ABG≌△CBE(SAS),∴AG=CE;
(2)如图所示:∵△ABG≌△CBE,∴∠BAG=∠BCE.
∵∠ABC=90°,∴∠BAG+∠AMB=90°.
∵∠AMB=∠CMN,∴∠BCE+∠CMN=90°,∴∠CNM=90°,∴AG⊥CE.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线相交于P,∠A=m°,
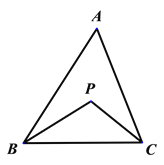
(1)若∠A=40°,求∠BPC的度数;
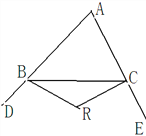
(2)设△ABC的外角∠CBD、∠BCE的平分线相交于Q, 且∠A=m°,求∠BQC的度数

(3)设△ABC的外角∠CBD、∠BCE的n等分线相交于R,且∠A=m°,∠CBR=![]() ∠CBD,∠BCR=
∠CBD,∠BCR=![]() ∠BCE,求∠BRC的度数
∠BCE,求∠BRC的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
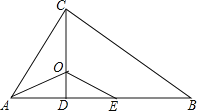
【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△A0E;
(2)求证:OE∥BC。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
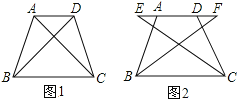
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
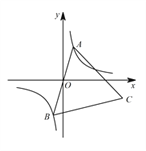
【题目】如图,已知点 ![]() 是双曲线
是双曲线 ![]() 在第三象限分支上的一个动点,连接
在第三象限分支上的一个动点,连接 ![]() 并延长交另一分支于点
并延长交另一分支于点 ![]() ,以
,以 ![]() 为边作等边三角形
为边作等边三角形 ![]() ,点
,点 ![]() 在第四象限内,且随着点
在第四象限内,且随着点 ![]() 的运动,点
的运动,点 ![]() 的位置也在不断变化,但点
的位置也在不断变化,但点 ![]() 始终在双曲线
始终在双曲线 ![]() 上运动,则
上运动,则 ![]() 的值是_______________.
的值是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国政府从2007年起对职业中专在校生给予生活补贴,每位在校生每年补贴1500元某市预计2008年职业中专在校生人数是2007年的1.2倍,于是要在2007年的基础上增加补贴600万元。2008年该市职业中专在校生有多少万人?补贴多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE,CD分别为其角平分线且交于点O.
(1)当∠A=60°时,求∠BOC的度数;
(2)当∠A=100°时,求∠BOC的度数;
(3)当∠A=α时,求∠BOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com