
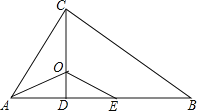
【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△A0E;
(2)求证:OE∥BC。
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)由AO平分∠BAC,可得∠CAO=∠EAO结合AO=AO,AE=AC即可由“SAS”证得:△AOC≌△AOE;
(2)由△AOC≌△AOE可得∠ACO=∠AEO,由∠ACB=90°,CD⊥AB于点D,易得∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,从而可得∠DCB=∠DOE,即可得到:OE∥BC.
试题解析:
(1)∵AO平分∠BAC,
∴∠CAO=∠EAO.
在△ACO和△AEO中:
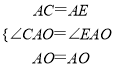 ,
,
∴△AOC≌△AOE.
(2)∵△AOC≌△AOE,
∴∠ACO=∠AEO,
∵ CD⊥AB于点D,
∴∠ODE=∠ACB=90°,
∴∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,
∴∠DCB=∠DOE,
∴OE∥BC.


科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】资料:小球沿直线撞击水平格档反弹时(不考虑垂直撞击),撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角.以图(1)为例,如果黑球 ![]() 沿从
沿从 ![]() 到
到 ![]() 方向在
方向在 ![]() 点处撞击
点处撞击 ![]() 边后将沿从
边后将沿从 ![]() 到
到 ![]() 方向反弹,根据反弹原则可知
方向反弹,根据反弹原则可知 ![]() ,即
,即 ![]() .如图(2)和(3),
.如图(2)和(3),![]() 是一个长方形的弹子球台面,有黑白两球
是一个长方形的弹子球台面,有黑白两球 ![]() 和
和 ![]() ,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)

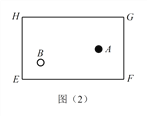
(1)探究(1):黑球 ![]() 沿直线撞击台边
沿直线撞击台边 ![]() 哪一点时,可以使黑球
哪一点时,可以使黑球 ![]() 经台边
经台边 ![]() 反弹一次后撞击到白球
反弹一次后撞击到白球 ![]() ?请在图(2)中画出黑球
?请在图(2)中画出黑球 ![]() 的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
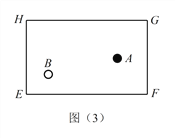
(2)探究(2):黑球 ![]() 沿直线撞击台边
沿直线撞击台边 ![]() 哪一点时,可以使黑球
哪一点时,可以使黑球 ![]() 先撞击台边
先撞击台边 ![]() 反弹一次后,再撞击台边
反弹一次后,再撞击台边 ![]() 反弹一次撞击到白球
反弹一次撞击到白球 ![]() ?请在图(3)中画出黑球
?请在图(3)中画出黑球 ![]() 的路线图,标出黑球撞击
的路线图,标出黑球撞击 ![]() 边的撞击点,简单说明作法,不用证明.
边的撞击点,简单说明作法,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
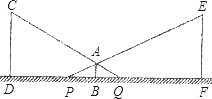
(1)小明距离路灯多远?
(2)求路灯高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
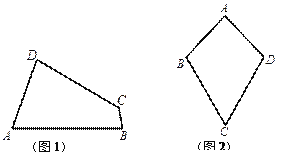
【题目】定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形![]() 是“等对角四边形”,
是“等对角四边形”, ![]() ,
, ![]() ,
, ![]() .求
.求![]() ,
, ![]() 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”![]() (如图2),其中
(如图2),其中![]() ,
, ![]() ,此时她发现
,此时她发现![]() 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”![]() 中,
中, ![]() ,
, ![]() ,AB=AD=4,.求∠D和对角线
,AB=AD=4,.求∠D和对角线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
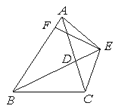
A.①②③ B.①③④ C.①②④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 为
为![]() 的直径,
的直径, ![]() 为弦
为弦![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
, ![]() .
.

(1)求证: ![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() 时,
时,
①求图中阴影部分的面积;
②以![]() 为原点,
为原点, ![]() 所在的直线为
所在的直线为![]() 轴,直径
轴,直径![]() 的垂直平分线为
的垂直平分线为![]() 轴,建立如图所示的平面直角坐标系,试在线段
轴,建立如图所示的平面直角坐标系,试在线段![]() 上求一点
上求一点![]() ,使得直线
,使得直线![]() 把阴影部分的面积分成
把阴影部分的面积分成![]() 的两部分.
的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com