
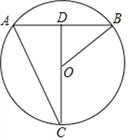
【题目】如图,点C在⊙O上,连接CO并延长交弦AB于点D,![]() ,连接AC、OB,若CD=8,AC=
,连接AC、OB,若CD=8,AC=![]() .
.
(1)求弦AB的长;
(2)求sin∠ABO的值.
【答案】(1)8;(2)![]() .
.
【解析】试题分析:
(1)由已知条件结合垂径定理易得CD⊥AB,从而可得∠ADC=90°,AB=2AD,结合AC=![]() ,CD=8可得AD=4,由此即可得到AB=8;
,CD=8可得AD=4,由此即可得到AB=8;
(2)设⊙O的为r,则由题意可得OB=r,OD=CD-r=8-r,结合BD=AD=4在Rt△OBD中由勾股定理建立方程,解方程即可求得x的值,从而可得OB和OD的长,这样由正弦函数的定义即可求得sin∠ABO的值.
试题解析:
(1)∵CD过圆心O,![]() ,
,
∴CD⊥AB,AB=2AD=2BD,
∵CD=40,AC=4![]() ,∠ADC=90°,
,∠ADC=90°,
∴AD=![]() ,
,
∴AB=2AD=8;
(2)设圆O的半径为r,则OD=8﹣r,
∵BD=AD=4,∠ODB=90°,
∴BD2+OD2=OB2,即42+(8﹣r)2=r2解得,r=5,OD=3,
∴sin∠ABO=![]() .
.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
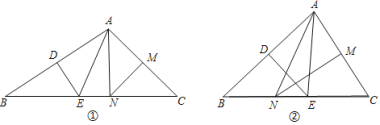
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2.则下列结论:①m<0,n>0;②直线y=nx+4n一定经过点(-4,0);③m与n满足m=2n-2;④当x>-2时,nx+4n>-x+m,其中正确结论的个数是( )
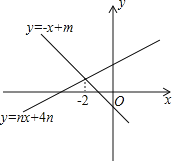
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
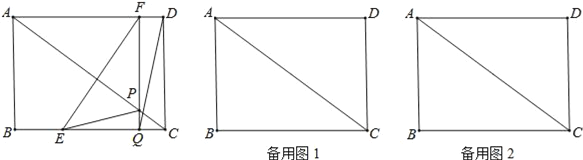
【题目】如图,在矩形ABCD中,AB=6cm,BC=8cm.如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为2cm/s和1cm/s.FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t(s)(0<t<4).
(1)连结EF、DQ,若四边形EQDF为平行四边形,求t的值;
(2)连结EP,设△EPC的面积为ycm2,求y与t的函数关系式,并求y的最大值;
(3)若△EPQ与△ADC相似,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明最喜欢吃芝麻馅的汤圆了,一天早晨小明妈妈给小明下了四个大汤圆,一个花生馅,一个水果馅,两个芝麻馅,四个汤圆除内部馅料不同外,其他一切均相同.
(1)求小明吃第一个汤圆恰好是芝麻馅的概率;
(2)请利用树状图或列表法,求小明吃前两个汤圆恰好是芝麻馅的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,直线y=x+1与双曲线![]() 的一个交点为P(m,6).
的一个交点为P(m,6).
(1)求k的值;
(2)M(2,a),N(n,b)分别是该双曲线上的两点,直接写出当a>b时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在口ABCD中,AE⊥BC于点E,AF⊥CD于点F,且AE=3cm,AF=5cm.若口ABCD的周长为32cm,则口ABCD的面积为( )
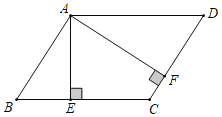
A. 24cm2B. 30cm2C. 64cm2D. 108cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。
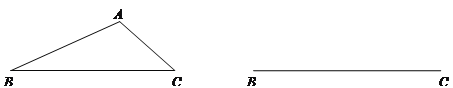
查看答案和解析>>
科目:初中数学 来源: 题型:
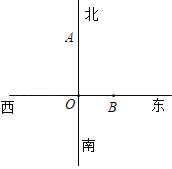
【题目】如图,一艘货轮位于O地,发现灯塔A在它的正北方向上,这艘货轮沿正东方向航行50千米,到达B地,此时用雷达测得灯塔A与货轮的距离为100千米.
(1)在图中作出灯塔A的位置,并作射线BA;
(2)以正北,正南方向为基准,借助量角器,描述灯塔A在B地的什么方向上(精确到1°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com