
����Ŀ�����壺�����������������![]() ������
������ ![]() ȡͬһ��ֵ��ʹ��
ȡͬһ��ֵ��ʹ��![]() ����ô��
����ô�� ![]() Ϊ��������ͨ���������ƶ�Ӧ��
Ϊ��������ͨ���������ƶ�Ӧ��![]() ֵΪ
ֵΪ![]() �������������� �����������������
�������������� �����������������![]() Ϊ��������ͨ����������ô
Ϊ��������ͨ����������ô![]() �����ֵ��Ϊ
�����ֵ��Ϊ![]() ������ֵͨ��.
������ֵͨ��.
��1���жϺ���![]() ��
��![]() �Ƿ�Ϊ����ͨ����������������ǣ������
�Ƿ�Ϊ����ͨ����������������ǣ������![]() ʱ���ǵ�������������������ǣ���˵�����ɣ�
ʱ���ǵ�������������������ǣ���˵�����ɣ�
��2����![]() ʱ����֪����
ʱ����֪����![]() ��
��![]() ����������ͨ������.����Ψһ������������
����������ͨ������.����Ψһ������������
�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�������ǵ�����ֵͨ��Ϊ18 ������� ![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ��
��![]() �ǻ�����ͨ������������Ϊ
�ǻ�����ͨ������������Ϊ![]() ��
��![]() ����2������
����2������![]() ��
��![]() ʱ����
ʱ����![]() ��ֵΪ
��ֵΪ![]() ��3
��3
��������
(1)��������ʽ��ȥy���õ�����x�ķ��̣���������ʵ��������������Ϊ����������������m=2���뺯������������ʽ���x��ֵ��Ϊ�����㣻
(2)�ٵ�![]() ʱ�����m��ֵ����
ʱ�����m��ֵ����![]() ʱ�ǻ�����ͨ�������������x,y��ֵ�����ɽ��
ʱ�ǻ�����ͨ�������������x,y��ֵ�����ɽ��
�ڹ�Ӯ�㼴Ϊ![]() �����ֵ,��
�����ֵ,��![]() �Ƕ��κ����ҿ������ϣ��������ֵ�ڶ˵���ã��ֱ�
�Ƕ��κ����ҿ������ϣ��������ֵ�ڶ˵���ã��ֱ�![]() ��
��![]() �������ʽ������ֵ����18���õ�����m�ķ�����⼴�ɡ�
�������ʽ������ֵ����18���õ�����m�ķ�����⼴�ɡ�
��1��������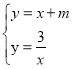
��![]()
��![]()
��![]() �������������
�������������
��![]() ��
��![]() Ϊ������ͨ����
Ϊ������ͨ����
��![]() ʱ��
ʱ��![]()
��![]()
�����Ϊ![]() ��
��![]()
��2���ٵ�![]() ʱ��
ʱ��
![]() ��
��![]()
�൱![]() ʱ�ǻ�����ͨ������
ʱ�ǻ�����ͨ������![]()
��������Ϊ![]()
��![]() ��
��![]() ʱ��������������ͨ������
ʱ��������������ͨ������
�������⣬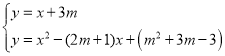
��![]()
��![]()
![]()
![]()
��![]() ��
��![]()
��![]() ��
��![]() ʱ��
ʱ��![]()
![]()
![]()
![]() ���ᣩ
���ᣩ
��![]() ʱ��
ʱ��![]()
![]() ���ᣩ
���ᣩ![]()
��![]() ��ֵΪ
��ֵΪ![]() ��3
��3


 ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC����CA=CB����ACB=90�㣬ֱ��l������C��AF��l�ڵ�F��BE��l�ڵ�E��
��1����֤����ACF�ա�CBE��
��2����ֱ����ת����ͼ2��ʾλ������D��AB���е�������DE����AB=![]() ����CBE=30�㣬��DE�ij���
����CBE=30�㣬��DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪A��O��B������ͬһֱ���ϣ�����OD��OE�ֱ�ƽ�֡�AOC����BOC
��1�����DOE�Ķ�����
��2����ͼ2���ڡ�AOD����һ������OF��ʹ��COF=![]() ���������䣬���DOF=
���������䣬���DOF=![]()
![]() ��
��
�����AOF�Ķ������ú�![]() �Ĵ���ʽ��ʾ��.
�Ĵ���ʽ��ʾ��.
������BOD�ǡ�AOF��2�������DOF�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ�����ʽ����ۺ������ɼ�Ϊx�֣�����Ϊ100�֣��涨��85��x��100ΪA����75��x��85ΪB����60��x��75ΪC����x��60ΪD�����������ȡ������ѧ����ѧ�����ۺ������ɼ����������Ƴ�����������������ͳ��ͼ�������ͼ�е���Ϣ������������⣺

(1)����ε����У�һ����ȡ��________��ѧ����a��________%��
(2)��ȫ����ͳ��ͼ��
(3)����ͳ��ͼ��C����Ӧ��Բ�Ľ�Ϊ________�ȣ�
(4)����У����2 000��ѧ����������Ƹ�УD��ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ������Rt��ABC��ֱ��ΪCE�İ�ԲO��ͼ1�ڷ�����B=90�㣬AC=2CE=m��BC=n����ԲO��BC���ڵ�D������ԲO�Ƶ�C����ʱ�뷽����ת����D���ԲO��ת����ECDʼ�յ�����ACB����ת�Ǽ�Ϊ����0��ܦ���180�㣩��
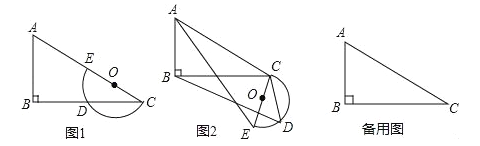
��1������=0��ʱ������DE������CDE=�� ���㣬CD=�� ����
��2�����ж�����ת������![]() �Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
�Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
��3����m=10��n=8������ת�ĽǶ���ǡΪ��ACB�Ĵ�Сʱ�����߶�BD�ij���
��4����m=6��n=![]() ������ԲO��ת������ABC�ı�����ʱ��ֱ��д���߶�BD�ij���
������ԲO��ת������ABC�ı�����ʱ��ֱ��д���߶�BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
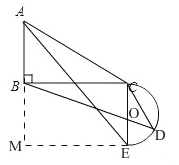
����Ŀ����ͼ��Rt��ABC����C=90�㣬CA=CB=4![]() cm����PΪAB���ϵ�һ�����㣬��E��CA�ߵ��е�, ����PE����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy cm.С������ѧϰ�����ľ��飬�Ժ���
cm����PΪAB���ϵ�һ�����㣬��E��CA�ߵ��е�, ����PE����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy cm.С������ѧϰ�����ľ��飬�Ժ���![]() ���Ա���
���Ա���![]() �ı仯���仯�Ĺ��ɽ�����̽����
�ı仯���仯�Ĺ��ɽ�����̽����
������С����̽�����̣��벹��������
��1��ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
��˵������ȫ����ʱ�����ֵ����һλС����
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺
��д���ú�����һ�����ʣ� ��
�ڵ�![]() ʱ��
ʱ��![]() �ij���ԼΪ cm.
�ij���ԼΪ cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֪ʶ��
�����dz�����ѧ��һ����Ҫ���ߣ�����������Խ�������������ϣ��о��������Ƿ�����������Ҫ�Ĺ���:
���磬��������![]() �㡢
�㡢![]() ���ʾ�����ֱ�Ϊ
���ʾ�����ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ����֮��ľ���
����֮��ľ���![]() ���߶�
���߶�![]() ���е�
���е�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ��
��
�������龳��
�������ϣ���![]() ��ʾ����Ϊ-20����
��ʾ����Ϊ-20����![]() ��ʾ����Ϊ10������
��ʾ����Ϊ10������![]() �ӵ�
�ӵ�![]() �����������������˶���ͬʱ������
�����������������˶���ͬʱ������![]() Ҳ�ӵ�
Ҳ�ӵ�![]() ���������Ḻ�����˶�����֪�˶���4����ʱ��
���������Ḻ�����˶�����֪�˶���4����ʱ��![]() ��
��![]() �����������Ҷ���
�����������Ҷ���![]() ��
��![]() �˶����ٶ�֮����
�˶����ٶ�֮����![]() ���ٶȵ�λ:��λ����/�룩��
���ٶȵ�λ:��λ����/�룩��
![]()
![]()
����ͼ
���ۺ����ã�
��1����![]() ���˶��ٶ�Ϊ______��λ����/�룬��
���˶��ٶ�Ϊ______��λ����/�룬��![]() ���˶��ٶ�Ϊ______��λ����/�룻
���˶��ٶ�Ϊ______��λ����/�룻
��2����![]() ʱ�����˶�ʱ�䣻
ʱ�����˶�ʱ�䣻
��3������![]() ��
��![]() �������������ԭ�����ٶ����������˶������˶��ķ����ޣ����Ƿ���:���Ŷ���
�������������ԭ�����ٶ����������˶������˶��ķ����ޣ����Ƿ���:���Ŷ���![]() ��
��![]() ���˶����߶�
���˶����߶�![]() ���е�
���е�![]() Ҳ�����˶����ʵ�
Ҳ�����˶����ʵ�![]() �ܷ���ԭ���غϣ����ܣ������
�ܷ���ԭ���غϣ����ܣ������![]() ��
��![]() ���������˶�ʱ�䣬��ֱ��д����
���������˶�ʱ�䣬��ֱ��д����![]() ���˶�������˶��ٶȣ������ܣ���˵�����ɣ�
���˶�������˶��ٶȣ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
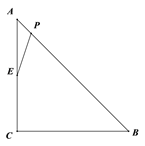
����Ŀ����֪x�����е�A��1��0������B��y���ϣ���C��m��0��Ϊx����һ������m����1������AB��BC��tan��ABO=![]() �����߶�BCΪֱ������M��ֱ��AB�ڵ�D������B��ֱ��l��AC����A��B��C�����������Ϊy=ax2+bx+c��ֱ��l�������ߺ͡�M����һ������ֱ���E��F��
�����߶�BCΪֱ������M��ֱ��AB�ڵ�D������B��ֱ��l��AC����A��B��C�����������Ϊy=ax2+bx+c��ֱ��l�������ߺ͡�M����һ������ֱ���E��F��
��1����B�����ꣻ
��2���ú�m��ʽ�ӱ�ʾ�����ߵĶԳ��
��3���߶�EF�ij��Ƿ�Ϊ��ֵ������ǣ����EF�ij���������ǣ�˵�����ɣ�
��4���Ƿ���ڵ�C��m��0����ʹ��BD=![]() AB�������ڣ������ʱm��ֵ���������ڣ�˵�����ɣ�
AB�������ڣ������ʱm��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ľ����������������Ӧ�����IJ�ľ���ֵ��������ͼ��ʾ����A��B�������Ϸֱ��Ӧ����Ϊa��b����A��B�����ľ����ʾΪ|AB|=|a��b|��
![]()
��������֪ʶ���⣺
��1��������������A��B��ʾ����Ϊx����1��
��A��B֮��ľ�����ú�x��ʽ�ӱ�ʾΪ������
����������֮��ľ���Ϊ2����ôxֵΪ������
��2��|x+1|+|x��2|����СֵΪ��������ʱx��ȡֵ��������
��3����֪��|x+1|+|x��2|����|y��3|+|y+2|��=15����x��2y�����ֵ������Сֵ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com