
ЁОЬтФПЁПЦНУцЩЯЃЌRtЁїABCгыжБОЖЮЊCEЕФАыдВOШчЭМ1АкЗХЃЌЁЯB=90ЁуЃЌAC=2CE=mЃЌBC=nЃЌАыдВOНЛBCБпгкЕуDЃЌНЋАыдВOШЦЕуCАДФцЪБеыЗНЯђа§зЊЃЌЕуDЫцАыдВOа§зЊЧвЁЯECDЪМжеЕШгкЁЯACBЃЌа§зЊНЧМЧЮЊІСЃЈ0ЁуЁмІСЁм180ЁуЃЉЃЎ
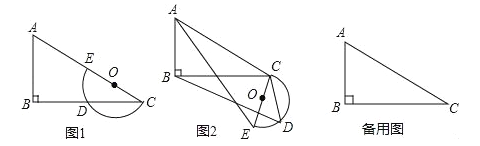
ЃЈ1ЃЉЕБІС=0ЁуЪБЃЌСЌНгDEЃЌдђЁЯCDE=ЁЁ ЁЁЁуЃЌCD=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉЪдХаЖЯЃКа§зЊЙ§ГЬжа![]() ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЛ
ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЛ
ЃЈ3ЃЉШєm=10ЃЌn=8ЃЌЕБа§зЊЕФНЧЖШІСЧЁЮЊЁЯACBЕФДѓаЁЪБЃЌЧѓЯпЖЮBDЕФГЄЃЛ
ЃЈ4ЃЉШєm=6ЃЌn=![]() ЃЌЕБАыдВOа§зЊжСгыЁїABCЕФБпЯрЧаЪБЃЌжБНгаДГіЯпЖЮBDЕФГЄЃЎ
ЃЌЕБАыдВOа§зЊжСгыЁїABCЕФБпЯрЧаЪБЃЌжБНгаДГіЯпЖЮBDЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ90ЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌЮоБфЛЏЃЌЃЈ3ЃЉBD=
ЃЌЮоБфЛЏЃЌЃЈ3ЃЉBD=![]() ЃЛЃЈ4ЃЉМДЃКBD=
ЃЛЃЈ4ЃЉМДЃКBD=![]() Лђ
Лђ![]() ЃЎ
ЃЎ
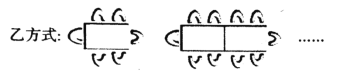
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйИљОнжБОЖЕФаджЪЃЌгЩDEЁЮABЕУ![]() МДПЩНтОіЮЪЬтЃЎЂкЧѓГіBDЁЂAEМДПЩНтОіЮЪЬтЃЎ
МДПЩНтОіЮЪЬтЃЎЂкЧѓГіBDЁЂAEМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉжЛвЊжЄУїЁїACEЁзЁїBCDМДПЩЃЎ
ЃЈ3ЃЉЧѓГіABЁЂAEЃЌРћгУЁїACEЁзЁїBCDМДПЩНтОіЮЪЬтЃЎ
ЃЈ4ЃЉЗжРрЬжТлЃКЂйШчЭМ5жаЃЌЕБІС=90ЁуЪБЃЌАыдВгыACЯрЧаЃЌЂкШчЭМ6жаЃЌЕБІС=90Ёу+ЁЯACBЪБЃЌАыдВгыBCЯрЧаЃЌЗжБ№ЧѓГіBDМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉНтЃКЂйШчЭМ1жаЃЌЕБІС=0ЪБЃЌСЌНгDEЃЌдђЁЯCDE=90ЁуЃЎЁпЁЯCDE=ЁЯB=90ЁуЃЌЁрDEЁЮABЃЌЁр![]() =
=![]() ЃЎЁпBC=nЃЌЁрCD=
ЃЎЁпBC=nЃЌЁрCD=![]() ЃЎЙЪД№АИЮЊЃК90ЁуЃЌ
ЃЎЙЪД№АИЮЊЃК90ЁуЃЌ![]() nЃЎ
nЃЎ
ЂкШчЭМ2жаЃЌЕБІС=180ЁуЪБЃЌBD=BC+CD=![]() nЃЌAE=AC+CE=
nЃЌAE=AC+CE=![]() mЃЌЁр
mЃЌЁр![]() =
=![]() ЃЎЙЪД№АИЮЊЃК
ЃЎЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМ3жаЃЌЁпЁЯACB=ЁЯDCEЃЌЁрЁЯACE=ЁЯBCDЃЎЁп![]() ЃЌЁрЁїACEЁзЁїBCDЃЌЁр
ЃЌЁрЁїACEЁзЁїBCDЃЌЁр![]() ЃЎ
ЃЎ
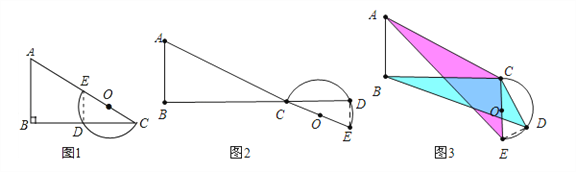
ЃЈ3ЃЉШчЭМ4жаЃЌЕБІС=ЁЯACBЪБЃЎдкRtЁїABCжаЃЌЁпAC=10ЃЌBC=8ЃЌЁрAB=![]() =6ЃЎдкRtЁїABEжаЃЌЁпAB=6ЃЌBE=BCЉCE=3ЃЌЁрAE=
=6ЃЎдкRtЁїABEжаЃЌЁпAB=6ЃЌBE=BCЉCE=3ЃЌЁрAE=![]() =
=![]() =3
=3![]() ЃЌгЩЃЈ2ЃЉПЩжЊЁїACEЁзЁїBCDЃЌЁр
ЃЌгЩЃЈ2ЃЉПЩжЊЁїACEЁзЁїBCDЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() =
=![]() ЃЌЁрBD=
ЃЌЁрBD=![]() ЃЎЙЪД№АИЮЊЃК
ЃЎЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ
ЃЈ4ЃЉЁпm=6ЃЌn=![]() ЃЌЁрCE=3ЃЌCD=2
ЃЌЁрCE=3ЃЌCD=2![]() ЃЌAB=
ЃЌAB=![]() =2ЃЌЂйШчЭМ5жаЃЌЕБІС=90ЁуЪБЃЌАыдВгыACЯрЧаЃЎдкRtЁїDBCжаЃЌBD=
=2ЃЌЂйШчЭМ5жаЃЌЕБІС=90ЁуЪБЃЌАыдВгыACЯрЧаЃЎдкRtЁїDBCжаЃЌBD=![]() =
=![]() =2
=2![]() ЃЎ
ЃЎ
ЂкШчЭМ6жаЃЌЕБІС=90Ёу+ЁЯACBЪБЃЌАыдВгыBCЯрЧаЃЌзїEMЁЭABгкMЃЎЁпЁЯM=ЁЯCBM=ЁЯBCE=90ЁуЃЌЁрЫФБпаЮBCEMЪЧОиаЮЃЌЁр![]() ЃЌЁрAM=5ЃЌAE=
ЃЌЁрAM=5ЃЌAE=![]() =
=![]() ЃЌгЩЃЈ2ЃЉПЩжЊ
ЃЌгЩЃЈ2ЃЉПЩжЊ![]() =
=![]() ЃЌЁрBD=
ЃЌЁрBD=![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК2![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧдкЁЖгаРэЪ§ЁЗетвЛеТжабЇЯАЙ§ОјЖджЕЕФИХФюЃК
вЛАуЕФЃЌЪ§жсЩЯБэЪОЪ§![]() ЕФЕугыдЕуЕФОрРыНазіЪ§
ЕФЕугыдЕуЕФОрРыНазіЪ§![]() ЕФОјЖджЕЃЌМЧзї
ЕФОјЖджЕЃЌМЧзї![]() .
.
ЪЕМЪЩЯЃЌЪ§жсЩЯБэЪОЪ§![]() ЕФЕугыдЕуЕФОрРыПЩМЧзї
ЕФЕугыдЕуЕФОрРыПЩМЧзї![]() ЃЌЪ§жсЩЯБэЪОЪ§
ЃЌЪ§жсЩЯБэЪОЪ§![]() ЕФЕугыБэЪОЪ§2ЕФЕуЕФОрРыПЩМЧзї
ЕФЕугыБэЪОЪ§2ЕФЕуЕФОрРыПЩМЧзї![]() ЃЌФЧУД:
ЃЌФЧУД:
ЃЈ1ЃЉЂйЪ§жсЩЯБэЪОЪ§3ЕФЕугыБэЪОЪ§1ЕФЕуЕФОрРыПЩМЧзї .
ЂкЪ§жсЩЯБэЪОЪ§![]() ЕФЕугыБэЪОЪ§2ЕФЕуЕФОрРыПЩМЧзї .
ЕФЕугыБэЪОЪ§2ЕФЕуЕФОрРыПЩМЧзї .
ЂлЪ§жсЩЯБэЪОЪ§![]() ЕФЕугыБэЪОЪ§
ЕФЕугыБэЪОЪ§![]() ЕФЕуЕФОрРыПЩМЧзї .
ЕФЕуЕФОрРыПЩМЧзї .
ЃЈ2ЃЉЪ§жсЩЯгыБэЪОЪ§![]() ЕФЕуЕФОрРыЮЊ5ЕФЕуга ИіЃЌЫќБэЪОЕФЪ§ЮЊ .
ЕФЕуЕФОрРыЮЊ5ЕФЕуга ИіЃЌЫќБэЪОЕФЪ§ЮЊ .
ЃЈ3ЃЉЭиеЙЃКЂйЕБЪ§![]() ШЁжЕЮЊ ЪБЃЌЪ§жсЩЯБэЪОЪ§
ШЁжЕЮЊ ЪБЃЌЪ§жсЩЯБэЪОЪ§![]() ЕФЕугыБэЪОЪ§
ЕФЕугыБэЪОЪ§![]() ЕФЕуЕФОрРызюаЁ.
ЕФЕуЕФОрРызюаЁ.
ЂкЕБећЪ§![]() ШЁжЕЮЊ ЪБЃЌЪНзг
ШЁжЕЮЊ ЪБЃЌЪНзг![]() газюаЁжЕЮЊ .
газюаЁжЕЮЊ .
ЂлЕБ![]() ШЁжЕЗЖЮЇЮЊ ЪБЃЌЪНзг
ШЁжЕЗЖЮЇЮЊ ЪБЃЌЪНзг![]() газюаЁжЕ.
газюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьШчЭМЫљЪОЕФЭМаЮЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉАДМзЗНЪННЋзРзгЦДдквЛЦ№ЃЎ
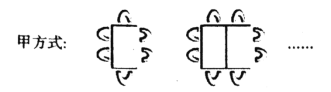
4еХзРзгЦДдквЛЦ№ЙВга ИізљЮЛЃЌnеХзРзгЦДдквЛЦ№ЙВга ИізљЮЛЃЛ
ЃЈ2ЃЉАДввЗНЪННЋзРзгЦДдквЛЦ№ЃЎ
6еХзРзгЦДдквЛЦ№ЙВга ИізљЮЛЃЌmеХзРзгЦДдквЛЦ№ЙВга ИізљЮЛЃЛ
ЃЈ3ЃЉФГЪГЬУгаAЃЌBСНИіВЭЬќЃЌЯжга102еХетбљЕФГЄЗНаЮзРзгЃЌМЦЛЎАбетаЉзРзгШЋЗХдкСНИіВЭЬќЃЌУПИіВЭЬќЖМвЊЗХгазРзг.НЋaеХзРзгЗХдкAВЭЬќЃЌАДМзЗНЪНУП6еХЦДГЩ1еХДѓзРзгЃЛНЋЦфгрзРзгЖМЗХдкBВЭЬќЃЌАДввЗНЪНУП4еХзРзгЦДГЩ1еХДѓзРзгЃЌШєСНИіВЭЬќвЛЙВга404ИізљЮЛЃЌЮЪAЃЌBСНИіВЭЬќИїгаЖрЩйИізљЮЛЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЫФБпаЮBDEFЪЧСтаЮЃЌЦфжаЁЯE=60ЁуЃЌНЋСтаЮBDEFШЦЕуBАДЫГЪБеыЗНЯђа§зЊЃЌМзЁЂввСНЮЛЭЌбЇЗЂЯждкДЫа§зЊЙ§ГЬжаЃЌгаШчЯТНсТлЃК
МзЃКЯпЖЮAFгыЯпЖЮCDЕФГЄЖШзмЯрЕШЃЛ
ввЃКжБЯпAFКЭжБЯпCDЫљМаЕФШёНЧЕФЖШЪ§ВЛБфЃЛ
ФЧУДЃЌФуШЯЮЊЃЈЁЁЁЁЃЉ
A. МзЁЂввЖМЖд B. ввЖдМзВЛЖд
C. МзЖдввВЛЖд D. МзЁЂввЖМВЛЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЖўДЮКЏЪ§
ЕФЭМЯѓгыЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЉЕФЭМЯѓНЛгк
ЮЊГЃЪ§ЃЉЕФЭМЯѓНЛгк![]() СНЕуЃЌЧвЕу
СНЕуЃЌЧвЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() .
.
ЃЈ1ЃЉЧѓГі![]() ЕФжЕМАЕу
ЕФжЕМАЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЩш![]() ЃЌШє
ЃЌШє![]() ЪБЃЌ
ЪБЃЌ![]() ЫцзХ
ЫцзХ![]() ЕФдіДѓЖјдіДѓЃЌЧв
ЕФдіДѓЖјдіДѓЃЌЧв![]() вВЫцзХ
вВЫцзХ![]() ЕФдіДѓЖјдіДѓЃЌЧѓ
ЕФдіДѓЖјдіДѓЃЌЧѓ![]() ЕФзюаЁжЕКЭ
ЕФзюаЁжЕКЭ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКЃЈЂЁЃЉШчЙћСНИіКЏЪ§![]() ЃЌДцдк
ЃЌДцдк ![]() ШЁЭЌвЛИіжЕЃЌЪЙЕУ
ШЁЭЌвЛИіжЕЃЌЪЙЕУ![]() ЃЌФЧУДГЦ
ЃЌФЧУДГЦ ![]() ЮЊЁАЛЅСЊЛЅЭЈКЏЪ§ЁБЃЌГЦЖдгІЕФ
ЮЊЁАЛЅСЊЛЅЭЈКЏЪ§ЁБЃЌГЦЖдгІЕФ![]() жЕЮЊ
жЕЮЊ![]() ЕФЁАЛЅСЊЕуЁБЃЛ ЃЈЂЂЃЉШчЙћСНИіКЏЪ§
ЕФЁАЛЅСЊЕуЁБЃЛ ЃЈЂЂЃЉШчЙћСНИіКЏЪ§![]() ЮЊЁАЛЅСЊЛЅЭЈКЏЪ§ЁБЃЌФЧУД
ЮЊЁАЛЅСЊЛЅЭЈКЏЪ§ЁБЃЌФЧУД![]() ЕФзюДѓжЕГЦЮЊ
ЕФзюДѓжЕГЦЮЊ![]() ЕФЁАЛЅЭЈжЕЁБ.
ЕФЁАЛЅЭЈжЕЁБ.
ЃЈ1ЃЉХаЖЯКЏЪ§![]() гы
гы![]() ЪЧЗёЮЊЁАЛЅЭЈЛЅСЊКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГі
ЪЧЗёЮЊЁАЛЅЭЈЛЅСЊКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГі![]() ЪБЫћУЧЕФЁАЛЅСЊЕуЁБЃЌШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЪБЫћУЧЕФЁАЛЅСЊЕуЁБЃЌШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌвбжЊКЏЪ§
ЪБЃЌвбжЊКЏЪ§![]() гы
гы![]() ЪЧЁАЛЅСЊЛЅЭЈКЏЪ§ЁБ.ЧвгаЮЈвЛЁАЛЅСЊЕуЁБЃЛ
ЪЧЁАЛЅСЊЛЅЭЈКЏЪ§ЁБ.ЧвгаЮЈвЛЁАЛЅСЊЕуЁБЃЛ
ЂйЧѓГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЂкШєЫћУЧЕФЁАЛЅЭЈжЕЁБЮЊ18 ЃЌЪдЧѓГі ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=5ЃЌAC=13ЃЌBCБпЩЯЕФжаЯпAD=6ЃЌдђЁїABDЕФУцЛ§ЪЧ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛМмГЄ2.5УзЕФЬнзгABаБППдкЪњжБЕФЧНACЩЯЃЌетЪБBЕНЧНACЕФОрРыЮЊ0.7УзЃЎ
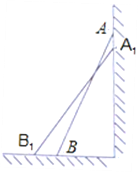
ЃЈ1ЃЉШєЬнзгЕФЖЅЖЫAбиЧНACЯТЛЌ0.9УзжСA1ДІЃЌЧѓЕуBЯђЭтвЦЖЏЕФОрРыBB1ЕФГЄЃЛ
ЃЈ2ЃЉШєЬнзгДгЖЅЖЫAДІбиЧНACЯТЛЌЕФОрРыЪЧЕуBЯђЭтвЦЖЏЕФОрРыЕФвЛАыЃЌЪдЧѓЬнзгбиЧНACЯТЛЌЕФОрРыЪЧЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаПМЬхг§ВтЪдЧАЃЌФГЧјНЬг§ОжЮЊСЫСЫНтбЁБЈв§ЬхЯђЩЯЕФГѕШ§ФаЩњЕФГЩМЈЧщПіЃЌЫцЛњГщВтСЫБОЧјВПЗжбЁБЈв§ЬхЯђЩЯЯюФПЕФГѕШ§ФаЩњЕФГЩМЈЃЌВЂНЋВтЪдЕУЕНЕФГЩМЈЛцГЩСЫЯТУцСНЗљВЛЭъећЕФЭГМЦЭМЃК
ЧыФуИљОнЭМжаЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ![]() ЃЉаДГіЩШаЮЭМжа
ЃЉаДГіЩШаЮЭМжа![]() __________
__________![]() ЃЌВЂВЙШЋЬѕаЮЭМЃЎ
ЃЌВЂВЙШЋЬѕаЮЭМЃЎ
ЃЈ![]() ЃЉдкетДЮГщВтжаЃЌВтЪдГЩМЈЕФжкЪ§КЭжаЮЛЪ§ЗжБ№ЪЧ__________ИіЁЂ__________ИіЃЎ
ЃЉдкетДЮГщВтжаЃЌВтЪдГЩМЈЕФжкЪ§КЭжаЮЛЪ§ЗжБ№ЪЧ__________ИіЁЂ__________ИіЃЎ
ЃЈ![]() ЃЉИУЧјЬхг§жаПМбЁБЈв§ЬхЯђЩЯЕФФаЩњЙВга
ЃЉИУЧјЬхг§жаПМбЁБЈв§ЬхЯђЩЯЕФФаЩњЙВга![]() ШЫЃЌШчЙћЬхг§жаПМв§ЬхЯђЩЯДя
ШЫЃЌШчЙћЬхг§жаПМв§ЬхЯђЩЯДя![]() ИівдЩЯЃЈКЌ
ИівдЩЯЃЈКЌ![]() ИіЃЉЕУТњЗжЃЌЧыФуЙРМЦИУЧјЬхг§жаПМжабЁБЈв§ЬхЯђЩЯЕФФаЩњФмЛёЕУТњЗжЕФгаЖрЩйУћЃП
ИіЃЉЕУТњЗжЃЌЧыФуЙРМЦИУЧјЬхг§жаПМжабЁБЈв§ЬхЯђЩЯЕФФаЩњФмЛёЕУТњЗжЕФгаЖрЩйУћЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com