
【题目】我们在《有理数》这一章中学习过绝对值的概念:
一般的,数轴上表示数![]() 的点与原点的距离叫做数
的点与原点的距离叫做数![]() 的绝对值,记作
的绝对值,记作![]() .
.
实际上,数轴上表示数![]() 的点与原点的距离可记作
的点与原点的距离可记作![]() ,数轴上表示数
,数轴上表示数![]() 的点与表示数2的点的距离可记作
的点与表示数2的点的距离可记作![]() ,那么:
,那么:
(1)①数轴上表示数3的点与表示数1的点的距离可记作 .
②数轴上表示数![]() 的点与表示数2的点的距离可记作 .
的点与表示数2的点的距离可记作 .
③数轴上表示数![]() 的点与表示数
的点与表示数![]() 的点的距离可记作 .
的点的距离可记作 .
(2)数轴上与表示数![]() 的点的距离为5的点有 个,它表示的数为 .
的点的距离为5的点有 个,它表示的数为 .
(3)拓展:①当数![]() 取值为 时,数轴上表示数
取值为 时,数轴上表示数![]() 的点与表示数
的点与表示数![]() 的点的距离最小.
的点的距离最小.
②当整数![]() 取值为 时,式子
取值为 时,式子![]() 有最小值为 .
有最小值为 .
③当![]() 取值范围为 时,式子
取值范围为 时,式子![]() 有最小值.
有最小值.
【答案】(1)①![]() ,②
,②![]() ,③
,③![]() ;(2)点有2个,分别为3,
;(2)点有2个,分别为3,![]() ;(3)①
;(3)①![]() ,3;②
,3;②![]() ;③
;③![]() .
.
【解析】
(1)由题意中的例子类比即可得出答案;
(2)分在表示数![]() 的点的左侧或右侧两种情况讨论即可;
的点的左侧或右侧两种情况讨论即可;
(3)根据点到点之间距离的最小时的相关情况求解即可.
(1)由题意可得:
①数轴上表示数3的点与表示数1的点的距离可记作![]() ;
;
②数轴上表示数![]() 的点与表示数2的点的距离可记作
的点与表示数2的点的距离可记作![]() ;
;
③数轴上表示数![]() 的点与表示数
的点与表示数![]() 的点的距离可记作
的点的距离可记作![]() ;
;
(2)当该点在![]() 左侧时,该点表示的数为:
左侧时,该点表示的数为:![]() ,
,
当该点在![]() 右侧时,该点表示的数为:
右侧时,该点表示的数为:![]() ;
;
故答案为:点有2个,分别为3,![]() ;
;
(3)①当数![]() 取值为
取值为![]() 时,数轴上表示数
时,数轴上表示数![]() 的点与表示数
的点与表示数![]() 的点的距离最小;
的点的距离最小;
②当整数![]() 取值为
取值为![]() 时,式子
时,式子![]() 有最小值为3;
有最小值为3;
③当![]() 取值范围为
取值范围为![]() 时,式子
时,式子![]() 有最小值.
有最小值.


科目:初中数学 来源: 题型:
【题目】北京时间2019年4月10日人类首次直接拍摄到黑洞的照片,它是一个“超巨型”质量黑洞,位于室女座星系团中一个超大质量星系﹣M87的中心,距离地球5500万光年.数据“5500万光年”用科学记数法表示为( )

A.5500×104光年B.055×108光年
C.5.5×103光年D.5.5×107光年
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣
,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣![]() 或﹣
或﹣![]() .其中正确的有_____.(请将正确结论的序号全部填在横线上)
.其中正确的有_____.(请将正确结论的序号全部填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图顺次连接等腰梯形四边中点得到一个四边形,再顺次连接所得四边形四边的中点得到的图形是( )
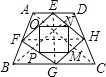
A. 等腰梯形B. 直角梯形C. 菱形D. 矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C、D四个车站的位置如图所示:

(1)求A、D两站的距离;
(2)求C、D两站的距离;
(3)比较A、C两站的距离与B、D两站的距离,哪两站的距离更大?大多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CA=CB,∠ACB=90°,直线l经过点C,AF⊥l于点F,BE⊥l于点E.
(1)求证:△ACF≌△CBE;
(2)将直线旋转到如图2所示位置,点D是AB的中点,连接DE.若AB=![]() ,∠CBE=30°,求DE的长.
,∠CBE=30°,求DE的长.
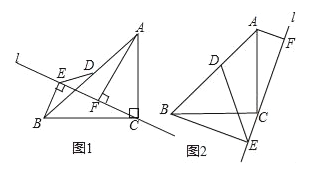
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°).
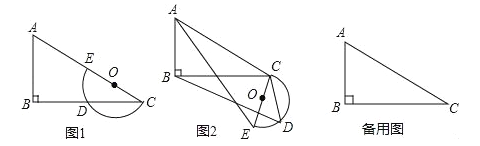
(1)当α=0°时,连接DE,则∠CDE= °,CD= ;
(2)试判断:旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)若m=10,n=8,当旋转的角度α恰为∠ACB的大小时,求线段BD的长;
(4)若m=6,n=![]() ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
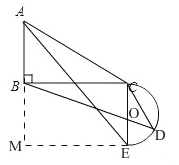
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com