
【题目】A、B、C、D四个车站的位置如图所示:

(1)求A、D两站的距离;
(2)求C、D两站的距离;
(3)比较A、C两站的距离与B、D两站的距离,哪两站的距离更大?大多少?
【答案】(1)6a+4b;(2)3a+2b;(3)B、D两站的距离更大,大2a-b.
【解析】
(1)根据两点间的距离列出代数式,合并即可得到结果;
(2)根据两点间的距离列出代数式,去括号合并即可得到结果;
(3)求出A、C两站的距离, 再用B、D两站的距离减去A、C两站的距离,根据计算结果即可求解.
解:(1)a+3b+5a+b=6a+4b.
故A、D两站的距离是6a+4b;
(2)5a+b-(2a-b)
=5a+b-2a+b
=3a+2b.
故C、D两站的距离是3a+2b;
(3)A、C两站的距离a+3b+2a-b=3a+2b,
则5a+b -(3a+2b)
=5a+b -3a-2b,
=2a-b
∵B、C两站的距离是2a-b,
∴2a-b>0.
故B、D两站的距离更大,大2a-b.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
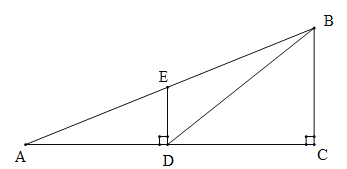
【题目】(本题满分6分)如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
查看答案和解析>>
科目:初中数学 来源: 题型:
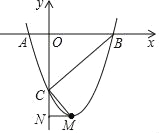
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).
(1)求该抛物线所对应的二次函数的表达式及顶点M的坐标;
(2)连结CB、CM,过点M作MN⊥y轴于点N,求证:∠BCM=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:(1)正整数和负整数统称为整数;(2)把能够写成分数形式![]() (m、n是整数,n≠0)的数叫做有理数;(3)异号两数相加,当绝对值不等时,取绝对值较大加数的符号,并用较大的加数减去较小的加数;(4)0是整数,但不是整式.正确的个数有 ( )
(m、n是整数,n≠0)的数叫做有理数;(3)异号两数相加,当绝对值不等时,取绝对值较大加数的符号,并用较大的加数减去较小的加数;(4)0是整数,但不是整式.正确的个数有 ( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在《有理数》这一章中学习过绝对值的概念:
一般的,数轴上表示数![]() 的点与原点的距离叫做数
的点与原点的距离叫做数![]() 的绝对值,记作
的绝对值,记作![]() .
.
实际上,数轴上表示数![]() 的点与原点的距离可记作
的点与原点的距离可记作![]() ,数轴上表示数
,数轴上表示数![]() 的点与表示数2的点的距离可记作
的点与表示数2的点的距离可记作![]() ,那么:
,那么:
(1)①数轴上表示数3的点与表示数1的点的距离可记作 .
②数轴上表示数![]() 的点与表示数2的点的距离可记作 .
的点与表示数2的点的距离可记作 .
③数轴上表示数![]() 的点与表示数
的点与表示数![]() 的点的距离可记作 .
的点的距离可记作 .
(2)数轴上与表示数![]() 的点的距离为5的点有 个,它表示的数为 .
的点的距离为5的点有 个,它表示的数为 .
(3)拓展:①当数![]() 取值为 时,数轴上表示数
取值为 时,数轴上表示数![]() 的点与表示数
的点与表示数![]() 的点的距离最小.
的点的距离最小.
②当整数![]() 取值为 时,式子
取值为 时,式子![]() 有最小值为 .
有最小值为 .
③当![]() 取值范围为 时,式子
取值范围为 时,式子![]() 有最小值.
有最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
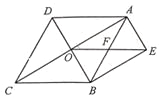
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
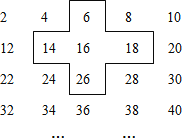
【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在日历中移动的规律后,突发奇想,将连续的得数2,4,6,8,…,排成如图形式:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)请你选择十字框中你喜欢的任意位置的一个数,将其设为x,并用含x的代数式表示十字框中五个数的和.
(2)若将十字框上下左右移动,可框住另外的五个数,试间:十字框能否框住和等于2015的五个数,如能,请求出这五个数;如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与二次函数
的图象与二次函数![]() (
(![]() 为常数)的图象交于
为常数)的图象交于![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() .
.
(1)求出![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)设![]() ,若
,若![]() 时,
时,![]() 随着
随着![]() 的增大而增大,且
的增大而增大,且![]() 也随着
也随着![]() 的增大而增大,求
的增大而增大,求![]() 的最小值和
的最小值和![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com