Question

【题目】2016四川省资阳市）已知抛物线与x轴交于A（6，0）、B（，0）两点，与y轴交于点C，过抛物线上点M（1，3）作MN⊥x轴于点N，连接OM．

（1）求此抛物线的解析式；

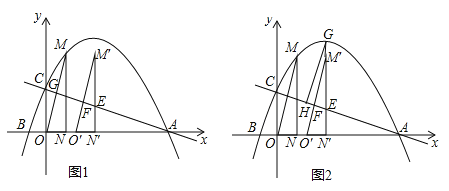
（2）如图1，将△OMN沿x轴向右平移t个单位（0≤t≤5）到△O′M′N′的位置，MN′、M′O′与直线AC分别交于点E、F．

①当点F为M′O′的中点时，求t的值；

②如图2，若直线M′N′与抛物线相交于点G，过点G作GH∥M′O′交AC于点H，试确定线段EH是否存在最大值？若存在，求出它的最大值及此时t的值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）①1；②t=2时，EH最大值为．

【解析】

试题分析：（1）设抛物线解析式为，把点M（1，3）代入即可求出a，进而解决问题．

（2））①如图1中，AC与OM交于点G．连接EO′，首先证明△AOC∽△MNO，推出OM⊥AC，在RT△EO′M′中，利用勾股定理列出方程即可解决问题．

②由△GHE∽△AOC得==，所以EG最大时，EH最大，构建二次函数求出EG的最大值即可解决问题．

试题解析：（1）设抛物线解析式为，把点M（1，3）代入得a=，∴抛物线解析式为，∴．

（2）①如图1中，AC与OM交于点G．连接EO′．∵AO=6，OC=2，MN=3，ON=1，∴=3，∴，∵∠AOC=∠MON=90°，∴△AOC∽△MNO，∴∠OAC=∠NMO，∵∠NMO+∠MON=90°，∴∠MON+∠OAC=90°，∴∠AGO=90°，∴OM⊥AC，∵△M′N′O′是由△MNO平移所得，∴O′M′∥OM，∴O′M′⊥AC，∵M′F=FO′，∴EM′=EO′，∵EN′∥CO，∴，∴，∴EN′=（5﹣t），在RT△EO′M′中，∵O′N′=1，EN′=（5﹣t），EO′=EM′=，∴，∴t=1．

②如图2中，∵GH∥O′M′，O′M′⊥AC，∴GH⊥AC，∴∠GHE=90°，∵∠EGH+∠HEG=90°，∠AEN′+∠OAC=90°，∠HEG=∠AEN′，∴∠OAC=∠HGE，∵∠GHE=∠AOC=90°，∴△GHE∽△AOC，∴，∴EG最大时，EH最大，∵EG=GN′﹣EN′===，∴t=2时，EG最大值=，∴EH最大值=，∴t=2时，EH最大值为．