
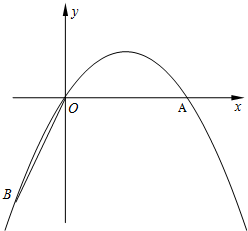
 如图,在直角坐标系中,点A的坐标为($2\sqrt{3}$,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
如图,在直角坐标系中,点A的坐标为($2\sqrt{3}$,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.分析 (1)作BC⊥OC于点C,由∠AOB=120°,∠AOC=90°,可得∠BOC=30°,由BO=AO=2$\sqrt{3}$,可得BC=$\sqrt{3}$,OC=3,即可得出点B的坐标,
(2)设抛物线的解析式为y=ax•(x-2$\sqrt{3}$),把点B代入即可求出抛物线的解析式,
(3)作PN⊥x轴,垂足为M,交AB于点N,设P(m,$-\frac{1}{3}{m^2}+\frac{{2\sqrt{3}}}{3}m$),可得M(m,0),由A,B的坐标,可求直线AB的解析式,可得N的坐标,从而得出PN的值,利用S△PAB=$\frac{1}{2}$PN×[2$\sqrt{3}$-(-$\sqrt{3}$)],即可得出最大值及点P的坐标.
解答 解:(1)如图1,作BC⊥OC于点C,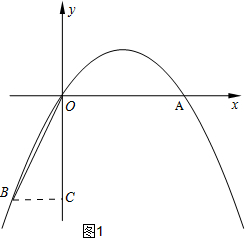
∵∠AOB=120°,∠AOC=90°,
∴∠BOC=30°,
∵BO=AO=2$\sqrt{3}$,
∴BC=$\sqrt{3}$,OC=3,
∴$B(-\sqrt{3},-3)$;
(2)设抛物线的解析式为y=ax•(x-2$\sqrt{3}$),
∵y=ax•(x-2$\sqrt{3}$),过B(-$\sqrt{3}$,-3),
∴-3=a×(-$\sqrt{3}$)×(-$\sqrt{3}$-2$\sqrt{3}$),
∴a=-$\frac{1}{3}$,
∴y=-$\frac{1}{3}$x2+$\frac{2}{3}\sqrt{3}$x,
(3)如图2,作PN⊥x轴,垂足为M,交AB于点N,设P(m,$-\frac{1}{3}{m^2}+\frac{{2\sqrt{3}}}{3}m$),则M(m,0),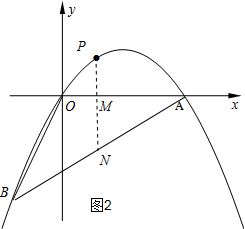 π
π
∵A($2\sqrt{3}$,0),B(-$\sqrt{3}$,-3),
∴直线AB的函数解析式为y=$\frac{\sqrt{3}}{3}$x-2,
∴N(m,$\frac{\sqrt{3}}{3}m$-2),
∴PN=-$\frac{1}{3}$m2+$\frac{2\sqrt{3}}{3}$m-($\frac{\sqrt{3}}{3}m$-2)=-$\frac{1}{3}$m2+$\frac{\sqrt{3}}{3}$m+2,
∵S△PAB=$\frac{1}{2}$PN×[2$\sqrt{3}$-(-$\sqrt{3}$)]
=$\frac{3\sqrt{3}}{2}$(-$\frac{1}{3}$m2+$\frac{\sqrt{3}}{3}$m+2)
=-$\frac{\sqrt{3}}{2}$m2+$\frac{3}{2}$m+3$\sqrt{3}$
=-$\frac{\sqrt{3}}{2}$(m-$\frac{\sqrt{3}}{2}$)2+$\frac{27\sqrt{3}}{8}$,
∴当m=$\frac{\sqrt{3}}{2}$时,最大值为S△PAB=$\frac{27\sqrt{3}}{8}$,
此时P($\frac{\sqrt{3}}{2}$,$\frac{3}{4}$).
点评 本题主要考查了二次函数的综合题,涉及直角三角形的性质,抛物线的关系式及最大值,解题的关键是求出点N的坐标,利用△PAB的面积列出一元二次方程求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
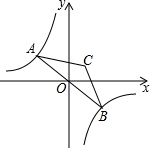 如图,点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为( )
如图,点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
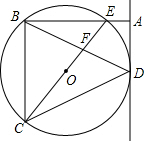 如图,⊙O为△BCD的外接圆,CE为⊙O的直径,过D作⊙O的切线交BE的延长线于A,且AD∥BC,BD交CE于F.
如图,⊙O为△BCD的外接圆,CE为⊙O的直径,过D作⊙O的切线交BE的延长线于A,且AD∥BC,BD交CE于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
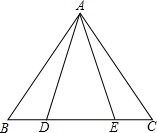 如图,△ABC中,点D、E在BC边上,∠BAD=∠CAE请你添加一对相等的线段或一对相等的角的条件,使△ABD≌△ACE.你所添加的条件是AB=AC.
如图,△ABC中,点D、E在BC边上,∠BAD=∠CAE请你添加一对相等的线段或一对相等的角的条件,使△ABD≌△ACE.你所添加的条件是AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com