
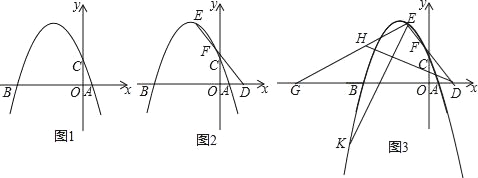
����Ŀ����ͼ1����֪������y=��![]() x2��
x2��![]() x+c��x���ཻ��A��B���㣨B����A�����ࣩ����y���ཻ��C�㣬��AB=10��
x+c��x���ཻ��A��B���㣨B����A�����ࣩ����y���ཻ��C�㣬��AB=10��
��1�������������ߵĽ���ʽ��
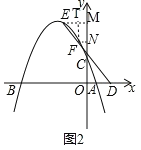
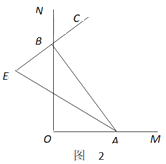
��2����ͼ2��D����x���ϣ�����A����Ҳ࣬E��Ϊ�������ϵڶ������ڵĵ㣬����ED���������ڵڶ������ڵ�����һ��F����E��y��ľ������F��y��ľ���֮��Ϊ3��1����֪tan��BDE=![]() �����E�����ꣻ
�����E�����ꣻ
��3����ͼ3���ڣ�2���������£���G��B��������x�Ḻ�����˶�������EG����H���߶�EG�ϣ�����DH����EDH=��EGB������E��EK��DH������������Ӧ��E����EK=EG�����K�����꣮
���𰸡���1��y=��![]() x2��
x2��![]() x+3����2��E����3��8������3��K(-11��-8).
x+3����2��E����3��8������3��K(-11��-8).
�������������������1���ȸ��ݺ�����ϵʽ����Գ��ᣬ��AB=10���������![]() �����꣬���뺯����ϵʽ���
�����꣬���뺯����ϵʽ���![]() ��ֵ�����ɽ��
��ֵ�����ɽ��
��2����EM��x�ᣬ����Ϊ��M��FN��x�ᣬ����Ϊ��N��FT��EM������Ϊ��T.�õ��ı���FTMNΪ���Σ���![]() ,
, ![]() ,�õ���BDE=��EFT������
,�õ���BDE=��EFT������![]() ����
����![]() �õ�
�õ�![]() ����
����![]() ���
���![]() ���뺯����ϵʽ���ɽ��
���뺯����ϵʽ���ɽ��
��3����EM��x�ᣬ����Ϊ��M������K��KR��ED����ED�ཻ�ڵ�R����x���ཻ�ڵ�Q.��֤�����EGM�ա�EKR�����![]()
![]() ֱ��RQ�Ľ���ʽΪ��
ֱ��RQ�Ľ���ʽΪ�� ![]() ���K������Ϊ
���K������Ϊ![]() ���������߽���ʽ�ɵ�x=11,�����ɽ��
���������߽���ʽ�ɵ�x=11,�����ɽ��
���������(1)��![]()
�ɵöԳ���Ϊx=4
��AB=10��
���A������Ϊ(1,0)��
![]() ��c=3
��c=3
�������ߵĽ���ʽΪ![]()
(2)��ͼ2����EM��x�ᣬ����Ϊ��M��FN��x�ᣬ����Ϊ��N��FT��EM������Ϊ��T.
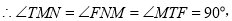
���ı���FTMNΪ���Σ�
��![]() ,
, ![]() ,
,
���BDE=��EFT��
![]()
![]()
��![]()
![]()
��![]() ����E.F��
����E.F��
��![]()
���m=0(��ȥ)��m=1��
��m=1ʱ��3m=3��
![]()
��E(3,8).
(3)��ͼ3����EM��x�ᣬ����Ϊ��M������K��KR��ED����ED�ཻ�ڵ�R����x���ཻ�ڵ�Q.

![]()
���KER=��GEM��
�ڡ�EGM�͡�EKR�У�
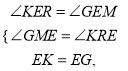
���EGM�ա�EKR��
��EM=ER=8��
![]()
��ED=10��
��DR=2��
![]()
![]() ����
����![]()
��ֱ��RQ�Ľ���ʽΪ�� ![]() ���K������Ϊ
���K������Ϊ![]() �����������߽���ʽ�ɵ�x=11,
�����������߽���ʽ�ɵ�x=11,
��K(11,8).


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90������A=30����CDΪ��ABC�����ߣ���CO��AB��O����E��CO�ӳ����ϣ�DE=AD������BE��DE��

��1����֤���ı���BCDEΪ���Σ�
��2������ABC�ָ������ȫ�ȵ������Σ���Ҫ�����ָ��߶Σ���AC=6���������ָ��߶γ��ȵĺͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�л����־�������A��B�����ͺŵ�ɨ�س���40�����Գ������й�·���������ɨ����֪1��A��ɨ�س���2��B��ɨ�س�ÿ�ܿ��Դ�����������100�֣�2��A��ɨ�س���1��B��ɨ�س�ÿ�ܿ��Դ�������110�֣�
��1����A��B�����ͺŵ�ɨ�س�ÿ��ÿ�ֱܷ���Դ����������ٶ֣�
��2����֪A��ɨ�س�ÿ���۸�Ϊ25��Ԫ��B��ɨ�س�ÿ���۸�Ϊ20��Ԫ��Ҫ��ʹ�����ֹ���ɨ�س����ʽ���910��Ԫ����ÿ�ܴ������������ֲ�����1400�֣������оٳ����й�������ָ�����ַ��������ʽ����٣������ʽ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶���ʵ��С��ȥij�̳�������Ʒ������������˽���̳���ÿ��80Ԫ�ļ۸���ijƷ�Ƴ���500��������ÿ��120Ԫ�ļ۸�������400�����̳�����ȡ������ʩ����ʣ�µij����������ۣ�
��1��ÿ���������۶���Ԫʱ�������������������ôﵽӯ��45%��Ԥ��Ŀ�ꣿ
��2���ڣ�1���������£�ij��˾��Ա�����������ڸ��̳�����Ǯ������20����Ʒ�Ƶij�������Ա��������Ϊ����Ա�����룬��Ҫ����5���ó�����������5������ʱǡ�ø��ϸ��̳����д��������ù�˾������25��������ƽ���۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ����
����![]() �ֱ�������
�ֱ�������![]() ���˶�(�����
���˶�(�����![]() �غ�)
�غ�)
�۲죺
(1)��ͼ1����![]() ��
��![]() ��ƽ���߽��ڵ�
��ƽ���߽��ڵ�![]() ��
��![]() _____��
_____��

���룺
(2)��ͼ2�����ŵ�![]() �ֱ�������
�ֱ�������![]() ���˶�(�����
���˶�(�����![]() �غ�). ��
�غ�). ��![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() �ķ����ӳ�����
�ķ����ӳ�����![]() ��ƽ���߽��ڵ�
��ƽ���߽��ڵ�![]() ,
, ![]() �Ĵ�С�����������ᣬ��
�Ĵ�С�����������ᣬ��![]() �Ķ����������ı�,˵������.
�Ķ����������ı�,˵������.
��չ��
(3)��ͼ3����(2)�����ϣ�С����![]() ��
��![]() �۵���ʹ��
�۵���ʹ��![]() �����ı���
�����ı���![]() �ڵ�
�ڵ�![]() ����λ�ã���
����λ�ã���![]() �Ķ���.
�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ѧС���������Ȼ�У�������������100ƪ�����������ȵķ���������Ϊ�������������黭��Ƶ���ֲ�ֱ��ͼ����ͼ������֪������5��С�����εĸߵı�Ϊl��3��7��6��3����ô����������б���Ϊ��������ģ��������ڻ����80��Ϊ���㣩��____ƪ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ԼԪ����ɽ���ס������˾����ĸ߶�y(m)���ɽʱ��x(min)֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ����������⣺
��1��t= min.
��2���������ٺ��ҵ�ɽ�������ٶ��Ǽ�ɽ�������ٶ�3����
�����ɽ�ĵ������ٶ��� m/min��
���������ɽ�����У������ĸ߶�y(m)���ɽʱ��x(min)֮��ĺ�����ϵʽ.
�����ס������˾����߶Ȳ�Ϊ70mʱ����x��ֵ��ֱ��д������������xֵ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��������е����������ж�����ƽ���ı��ε���( )
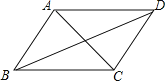
A. AB//CD, AD=BCB. ��B����C����A����D
C. AB=AD, BC=CDD. AB=CD, AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=3x+2��ͼ����y�ύ�ڵ�A���뷴��������y=![]() ��k��0���ڵ�һ�����ڵ�ͼ���ڵ�B���ҵ�B�ĺ�����Ϊ1������A��AC��y�ύ����������y=
��k��0���ڵ�һ�����ڵ�ͼ���ڵ�B���ҵ�B�ĺ�����Ϊ1������A��AC��y�ύ����������y=![]() ��k��0����ͼ���ڵ�C������BC��
��k��0����ͼ���ڵ�C������BC��
��1�����������ı���ʽ��
��2�����ABC�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com