Question

17．如图，在直角坐标系中，以点A（$\sqrt{3}$，0）为圆心，以2$\sqrt{3}$为半径的圆与x轴交于B，C两点，与y轴交于D，E两点．
（1）写出B，C，D点坐标（不写计算过程）
（2）若B、C、D三点在抛物线y=ax²+bx+c上，求这个抛物线的解析式．
（3）若圆A的切线交于x轴正半轴于点M，交y轴负半轴与点N，切点为P，∠OMN=30°，试判断直线MN是否经过所示抛物线的顶点？说明理由．

Answer 1

分析 （1）连接AD，构造直角三角形解答，在直角△ADO中，OA=$\sqrt{3}$，AD=2$\sqrt{3}$，根据勾股定理就可以求出AD的长，求出D的坐标，再利用圆的性质得出B，C的坐标．
（2）求出B、C、D的坐标，用待定系数法设出一般式解答；
（3）求出抛物线交点坐标，连接AP，则△APM是直角三角形，且AP等于圆的半径，根据三角函数就可以求出AM的长，已知OA，就可以得到OM，则M点的坐标可以求出；同理可以在直角△BNM中，根据三角函数求出BN的长，求出N的坐标，根据待定系数法就可以求出直线MN的解析式．将交点坐标代入直线解析式验证即可．

解答 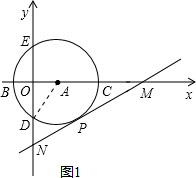解：（1）如图1，连接AD，得OA=$\sqrt{3}$，AD=2$\sqrt{3}$，
∴OD=$\sqrt{A{D}^{2}-O{A}^{2}}$=$\sqrt{（2\sqrt{3}）^{2}-（\sqrt{3}）^{2}}$=3，
∴D（0，-3），
∵点A（$\sqrt{3}$，0）为圆心，以2$\sqrt{3}$为半径的圆与x轴交于B、C两点，
∴B（-$\sqrt{3}$，0），C（3$\sqrt{3}$，0）；

（2）∵B（-$\sqrt{3}$，0），C（3$\sqrt{3}$，0），D（0，-3）
∴将B，C，D三点代入抛物线y=ax²+bx+c得，
$\left\{\begin{array}{l}{0=3a-\sqrt{3}b+c}\\{0=27a+3\sqrt{3}b+c}\\{c=-3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=-\frac{2}{3}\sqrt{3}}\\{c=-3}\end{array}\right.$
∴抛物线为：y=$\frac{1}{3}$x²-$\frac{2\sqrt{3}}{3}$x-3．

（3）如图2，连接AP，在Rt△APM中，∠PMA=30°，AP=2$\sqrt{3}$
∴AM=4$\sqrt{3}$
∴M（5$\sqrt{3}$，0）
∵ON=MO×tan30°=5$\sqrt{3}$
∴N（0，-5）
设直线MN的解析式为y=kx+b，由于点M（5$\sqrt{3}$，0）和N（0，-5）在直线MN上，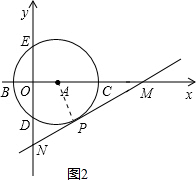
则$\left\{\begin{array}{l}{5\sqrt{3}k+b=0}\\{b=-5}\end{array}\right.$，
解得$\left\{\begin{array}{l}{b=-5}\\{k=\frac{\sqrt{3}}{3}}\end{array}\right.$
∴直线MN的解析式为y=$\frac{\sqrt{3}}{3}$x-5
∵抛物线的顶点坐标为（$\sqrt{3}$，-4），
当x=$\sqrt{3}$时，y=-4
∴点（$\sqrt{3}$，-4）在直线y=$\frac{\sqrt{3}}{3}$x-5上，即直线MN经过抛物线的顶点．

点评 此题主要考查了二次函数的综合应用以及用待定系数法求函数解析式和圆以及存在性问题相结合，培养了同学们的实际应用能力，注意利用数形结合得出是解题关键．