
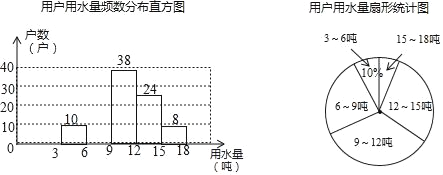
����Ŀ��ÿ���3��22��Ϊ���Ϲ�ȷ����������ˮ������ij����Ϊ��������Լ��ˮ���ӱ�����1000����ͥ�������ȡ���ּ�ͥ����������ÿ�µ���ˮ������������Ľ�����Ƴ����������в�������ͳ��ͼ��ÿ�����ݰ����Ҷ˵㵫��������˵㣩���������ͳ��ͼ����������⣺
��1���˴γ�������������������� ����
��2����ȫƵ���ֲ�ֱ��ͼ��������ͼ����6�֩���9�������ֵ�Բ�ĽǵĶ�����
��3���������ˮ��˾����������ˮ����Ϊÿ��ÿ��12�֣���������������ˮ���IJ������ܻ����۸�����������ˮ���IJ���ʵ�мӼ��շѣ���ô������û���Լ�ж��ٻ���ͥ�ܹ�ȫ�����ܻ����۸�
���𰸡���1��100����2����ͼ����������3��680��.
����������������1����3��6�ֵĻ�������ٷֱȿɵ�����������
��2���ܻ�����ȥ��������Ļ���֮�����6��9�ֵĻ��������ɲ�ȫֱ��ͼ����6��9�ֵĻ�����ռ��������360�ȿɵ�Բ�ĽǶ�����
��3���ܻ�������������3��12�ֵĻ�����ռ�������ɵã�
��⣺��1���˴γ������������������10��10%=100��
�ʴ�Ϊ��100��
��2��6��9�ֵĻ���Ϊ100����10+38+24+8��=20��������
��ȫƵ���ֲ�ֱ��ͼ���£�
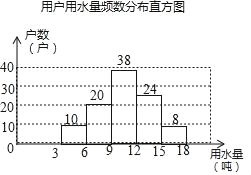
����ͼ����6�֩���9�������ֵ�Բ�ĽǵĶ���Ϊ360���![]() =72�㣻
=72�㣻
��3��1000��![]() =680��
=680��
�𣺸�����Լ��680����ͥ����ˮȫ�����ܻ����۸�


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E,F�ֱ�����ABCD�ı�BC,AD�ϵ��е㣬����BAC=90����
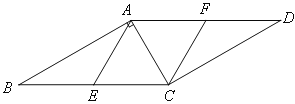
��1����֤���ı���AECF�����Σ�
��2������B=30����BC=10��������AECF�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬʱ������ö�ʵؾ��ȵ����ӣ����ӵ�������ֱ����1��6�ĵ��������ϵ���ĵ����У�һ�������ܱ���һ�����������ĸ����ǡ�
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪һ�κ���![]() ��ͼ����
��ͼ����![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() .��
.��![]() Ϊ���ڵ�һ������������
Ϊ���ڵ�һ������������![]() ����
����![]() ��
��![]() .��
.��![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() .
.

��1�����![]() �����ꣻ
�����ꣻ
��2������![]() ���ж��ı���
���ж��ı���![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3����ֱ��![]() ����һ��
����һ��![]() ��ʹ��
��ʹ��![]() �����
�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ǰ�һ����Բ�������ߵ�һ����Χ�ɵķ��ͼ�γ�Ϊ����Բ������֪��A��B��C��D�ֱ�������Բ����������Ľ��㣬�����ߵĽ���ʽΪy��x2��2x��3��ABΪ��Բ��ֱ�������������Բ����y��صõ���CD�ij�Ϊ____��
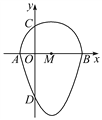
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ������г���ѧҵˮƽ��������ѧ�Ƶ�Ů��800�����������У�ij����ͬʱ���ܵ�СӨ��С÷���ܵ�·��S���ף�������ʱ��t���룩֮��ĺ���ͼ��ֱ�Ϊ�߶�OA������OBCD������˵����ȷ���ǣ�������

A��СӨ���ٶ���ʱ������������B��С÷��ƽ���ٶȱ�СӨ��ƽ���ٶȴ�
C�������ܺ�180��ʱ����������D�������ܺ�50��ʱ��С÷��СӨ��ǰ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
��ͼ����ƽ��ֱ������ϵ�У���֪������y��ax2��bx��8��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ(��2��0)��(6����8)��
(1)�������ߵĽ���ʽ�����ֱ������B�͵�E�����ꣻ
(2)��̽�����������Ƿ���ڵ�F��ʹ��FOE�ա�FCE.�����ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABCΪ�ȱ������Σ���DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ��������ADEF��A��D��E��F����ʱ�����У���ʹ��DAF=60����ֱ��EF��ֱ��BC����H.
��1����ͼ�٣�����D�ڱ�BC��ʱ����˵����![]() ��
��
��2����ͼ�ڣ�����D�ڱ�BC���ӳ�������������������ʱ������![]() ���Ƿ����������������˵�����ɣ�������������д��AD��DH��AC֮����ڵ�������ϵ��
���Ƿ����������������˵�����ɣ�������������д��AD��DH��AC֮����ڵ�������ϵ��
��3����ͼ�ۣ�����D�ڱ�CB���ӳ�������������������ʱ����ȫͼ�Σ���ֱ��д��AD��DH��AC֮����ڵ�������ϵ.
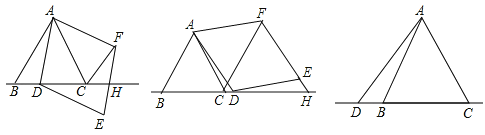
ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�У�AB��AC��AD��BC����ΪD.����ADC�Ƶ�D��ʱ����ת90����A����BD�ϵ�A1������C����DA�ӳ����ϵ�C1����A1C1��AB���ڵ�E.
��֤����A1BE�ա�AC1E.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com