
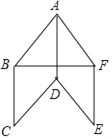
【题目】已知△ABC为等边三角形,点D为直线BC上一动点(点D不与B,C重合),以AD为边作菱形ADEF(A,D,E,F按逆时针排列),使∠DAF=60°,直线EF与直线BC交于H.
(1)如图①,当点D在边BC上时,试说明:![]() ;
;
(2)如图②,当点D在边BC的延长线上且其他条件不变时,结论![]() ;是否成立?若成立,请说明理由;若不成立,请写出AD、DH、AC之间存在的数量关系;
;是否成立?若成立,请说明理由;若不成立,请写出AD、DH、AC之间存在的数量关系;
(3)如图③,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AD、DH、AC之间存在的数量关系.
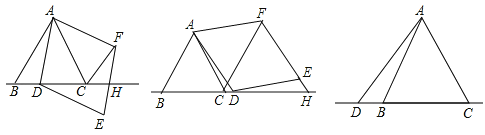
图1 图2 图3
【答案】(1)证明见解析;(2)成立;(3)补图见解析,数量关系![]() .
.
【解析】分析:(1)通过△ACD∽△DEH的对应边成比例得到![]() ,即
,即![]() =
=![]() ,则AD2=DHAC;
,则AD2=DHAC;
(2)图(2)中,AD2=DHAC仍然成立.易证△ACD∽△DEH,则该相似三角形的对应边成比例:![]() ,即
,即![]() =
=![]() ,则AD2=DHAC;
,则AD2=DHAC;
(3)如图3,解题思路同(2).易证△ACD∽△DEH,则该相似三角形的对应边成比例:![]() ,即
,即![]() =
=![]() ,则AD2=DHAC.
,则AD2=DHAC.
详解:(1)∵四边形ADEF是菱形,∠DAF=60°,
∴AD∥EF,∠DAF=∠E=60°,AD=DE,∴∠1=∠2.
∵△ABC是等边三角形,∴∠ACD=60°,∠ACD=∠E,∴△ACD∽△DEH,∴![]() ,即
,即![]() =
=![]() ,∴AD2=DHAC;
,∴AD2=DHAC;
(2)结论是:图(2)中,AD2=DHAC仍然成立.
理由如下:如图2.
∵在菱形ADEF中,AD∥EF,∠DAF=∠E=60°,AD=DE,∴∠ADC=∠DHE,∠DEF=120°.
又∵△ABC是等边三角形,∴∠ACB=60°,∴∠ACD=120°,∴∠ACD=∠DEH,∴△ACD∽△DEH,∴![]() ,即
,即![]() =
=![]() ,则AD2=DHAC;
,则AD2=DHAC;
(3)补全图形是如图3.数量关系AD2=DHAC.理由同(2).


科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
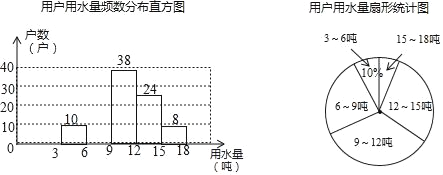
【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 ;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学将某班级毕业升学体育测试成绩(满分30分)统计整理,得到下表,则下列说法错误的是( )
分数 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
人数 | 2 | 4 | 3 | 8 | 10 | 9 | 6 | 3 | 1 |
A. 该组数据的众数是24分
B. 该组数据的平均数是25分
C. 该组数据的中位数是24分
D. 该组数据的极差是8分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直线y=﹣x沿y轴向下平移后的直线恰好经过点A(2,﹣4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
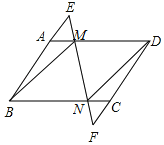
【题目】如图,已知平行四边形ABCD延长BA到点E,延长DC到点E,使得AE=CF,连结EF,分别交AD、BC于点M、N,连结BM,DN.
(1)求证:AM=CN;
(2)连结DE,若BE=DE,则四边形BMDN是什么特殊的四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com