
����Ŀ���ۺ���̽��
��ͼ����ƽ��ֱ������ϵ�У���֪������y��ax2��bx��8��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ(��2��0)��(6����8)��
(1)�������ߵĽ���ʽ�����ֱ������B�͵�E�����ꣻ
(2)��̽�����������Ƿ���ڵ�F��ʹ��FOE�ա�FCE.�����ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�

���𰸡�(1) y��![]() x2��3x��8����2����F������Ϊ(3��
x2��3x��8����2����F������Ϊ(3��![]() ����4)��(3��
����4)��(3��![]() ����4)��
����4)��
�������������������1����A��D������������߿���������ߵĺ�������ʽ���������ߵĶԳ��Կ����B�����꣬��D����������ֱ��OD�Ľ���ʽ��������E�����ꣻ
��2����ϣ�1����֪OE=CE����ȫ�������ε����ʿ�֪OF=CF����֪��F���߶�OC�Ĵ�ֱƽ�����ϣ�������F��������꣬���������߽���ʽ�����F������꣮
���������
��1����������y=ax2+bx-8������A��-2��0����D��6��-8����
��![]()
���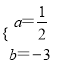
�������ߵĺ�������ʽΪy��![]() x23x8��
x23x8��
��y��![]() x23x8��
x23x8��![]() (x3)2
(x3)2![]() ��
��
�������ߵĶԳ���Ϊֱ��x=3��
����������x�ύ��A��B���㣬��A������Ϊ��-2��0����
���B��������8��0����
��ֱ��L�ĺ�������ʽΪy=kx��
�ߵ�D��6��-8����ֱ��L�ϣ�
��6k=-8�����k=-![]() ��
��
��ֱ��L�ĺ�������ʽΪy=-![]() x��
x��
�ߵ�EΪֱ��L�������߶Գ���Ľ��㣬
���E�ĺ�����Ϊ3��������Ϊ-![]() ��3=-4��
��3=-4��
���E��������3��-4����
��2���������ϴ��ڵ�F��ʹ��FOE�ա�FCE��
��OE=CE=5��
��FO=FC��
���F��OC�Ĵ�ֱƽ�����ϣ���ʱ��F��������Ϊ-4��
��![]() x2-3x-8=-4�����x=3��
x2-3x-8=-4�����x=3��![]() ��
��
���F��������3-![]() ��-4����3+
��-4����3+![]() ��-4����
��-4����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ʵ������ƶ����ij������ƶ�������ڵ��������Ĺػ��Ͱ�����Ͷ����һ������������һ���ľ�����ֳ������10�·ݴ������ﲶ���˲���ͻ��㹲2500ǧ�ˣ����г��ϲ�����ÿǧ��16Ԫ�ļ۸���ۣ�������ÿǧ��24Ԫ�ļ۸���ۣ�������ƶ����10�·�����52000Ԫ��
��1������10�·ݴ������ﲶ�̲���ͻ��������ǧ�ˣ�
��2����ƶ��������12�·��ٴδ������ﲶ�̣��������������ۼ۸��ϣ�����������10�·ݼ�����![]() ǧ�ˣ����ۼ۸䣻����������10�·ݼ�����
ǧ�ˣ����ۼ۸䣻����������10�·ݼ�����![]() �����ۼ۸��10�·ݼ�����
�����ۼ۸��10�·ݼ�����![]() ����ƶ������10�·ݺ�12�·����β����й�������94040Ԫ�������ﵽ����ƶ�¸�����
����ƶ������10�·ݺ�12�·����β����й�������94040Ԫ�������ﵽ����ƶ�¸�����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬��
��һ�㣬��![]() Ϊ������
������![]() ������
������![]() ƽ��
ƽ��![]()
��1����ͼ�٣�![]() ��
��![]() ��������ϵΪ______
��������ϵΪ______

��2����ͼ�٣����![]() ���������
���������![]() �Ķ�����˵�����ɣ�
�Ķ�����˵�����ɣ�
��3������ͼ���е�![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ�ڵ�λ�ã�
��ת��ͼ�ڵ�λ�ã�![]() ��Ȼƽ��
��Ȼƽ��![]() ����
����![]() ����ֱ��д��
����ֱ��д��![]() �Ķ���
�Ķ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���3��22��Ϊ���Ϲ�ȷ����������ˮ������ij����Ϊ��������Լ��ˮ���ӱ�����1000����ͥ�������ȡ���ּ�ͥ����������ÿ�µ���ˮ������������Ľ�����Ƴ����������в�������ͳ��ͼ��ÿ�����ݰ����Ҷ˵㵫��������˵㣩���������ͳ��ͼ����������⣺
��1���˴γ�������������������� ����
��2����ȫƵ���ֲ�ֱ��ͼ��������ͼ����6�֩���9�������ֵ�Բ�ĽǵĶ�����
��3���������ˮ��˾����������ˮ����Ϊÿ��ÿ��12�֣���������������ˮ���IJ������ܻ����۸�����������ˮ���IJ���ʵ�мӼ��շѣ���ô������û���Լ�ж��ٻ���ͥ�ܹ�ȫ�����ܻ����۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��BC���ӳ����ϣ���CE=BC��AE=AB��AE��DC�ཻ�ڵ�O������DE��
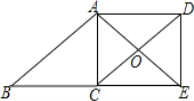
��1����֤���ı���ACED�Ǿ��Σ�
��2������AOD=120����AC=4����Խ���CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ij�༶��ҵ��ѧ�������Գɼ�������30�֣�ͳ���������õ��±���������˵��������ǣ�������
���� | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
���� | 2 | 4 | 3 | 8 | 10 | 9 | 6 | 3 | 1 |
A. �������ݵ�������24��
B. �������ݵ�ƽ������25��
C. �������ݵ���λ����24��
D. �������ݵļ�����8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijְҵ���л�����ѧ��42�ˣ���������������Ů��������2����3�ˣ�
��1���ð�������Ů�����ж����ˣ�
��2��ij�����������ð���¼30��ѧ���������ԣ��ð��С�Ů��ÿ���ܼӹ���������ֱ�Ϊ50����45����Ϊ��֤����ÿ��ӹ����������������1460������ô����Ҫ��¼��������ѧ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��y=��x��y������ƽ�ƺ��ֱ��ǡ�þ�����A��2����4��������y�ύ�ڵ�B����x���ϴ���һ��Pʹ��PA+PB��ֵ��С�����P������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�E��F�ֱ��DZ�AD��BC�ϵĵ㣬��AE=CF��ֱ��EF�ֱ�BA���ӳ��ߡ�DC���ӳ����ڵ�G��H����BD�ڵ�O��
��1����֤����ABE�ա�CDF��
��2������DG����DG=BG�����ı���BEDF��ʲô�����ı��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com