
【题目】将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转(0°<<120°)得到线段AD,连接CD.
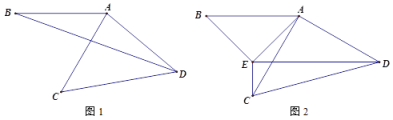
(1)连接BD,如图1,若=80°,则∠BDC的度数为 ;(直接写出结果)
(2)如图2,以AB为斜边作直角三角形ABE,使得∠B=∠ACD,连接CE,DE.若∠CED=90°,求的值.
【答案】(1)30°;(2)90°.
【解析】
(1)根据图形旋转的性质可知AB=AC=AD,再由圆周角定理即可得出结论;
(2)过点AM⊥CD于点M,连接EM,先根据AAS定理得出△AEB≌△AMC,故可得出AE=AM,∠BAE=∠CAM,所以△AEM是等边三角形.根据AC=AD,AM⊥CD可知CM=DM.故可得出点A、C、D在以M为圆心,MC为半径的圆上.由圆周角定理可得出结论.
解:(1)∵线段AC,AD由AB旋转而成,
∴AB=AC=AD.
∴点B、C、D在以A为圆心,AB为半径的圆上.
∴∠BDC=![]() ∠BAC=30°.
∠BAC=30°.
故答案为:30°;
(2)过点AM⊥CD于点M,连接EM.
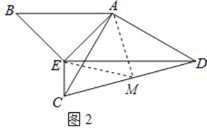
则∠AMD=∠AMC=90°.
在△AEB与△AMC中, ,
,
∴△AEB≌△AMC(AAS).
∴AE=AM,∠BAE=∠CAM.
∴∠EAM=∠EAC+∠CAM=∠EAC+∠BAE=∠BAC=60°.
∴△AEM是等边三角形.
∴EM=AM=AE.
∵AC=AD,AM⊥CD,
∴CM=DM.
又∵∠DEC=90°,
∴EM=CM=DM.
∴AM=CM=DM.
∴点A、C、D在以M为圆心,MC为半径的圆上.
∴=∠CAD=90°.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象G经过点A(4,1),直线l:y=
(x>0)的图象G经过点A(4,1),直线l:y=![]() +b与图象G交于点B,与y轴交于点C.
+b与图象G交于点B,与y轴交于点C.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为W.
①当b=﹣1时,直接写出区域W内的整点个数;
②若区域W内恰有4个整点,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
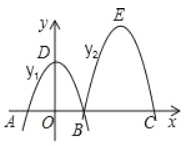
【题目】如图,抛物线y1的顶点在y轴上,y2由y1平移得到,它们与x轴的交点为A、B、C,且2BC=3AB=4OD=6,若过原点的直线被抛物线y1、y2所截得的线段长相等,则这条直线的解析式为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)过以下三个点:(m,n),(m+2,2n),和(m+6,n),当抛物线上另有点的横坐标为m+4时,它的纵坐标为_____;当横坐标为m﹣2时,它的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=5,AB=9.
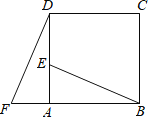
(1)求:DE的长度;
(2)求证:BE⊥DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三张完全相同且不透明的卡片正面分别写了﹣1,0,1三个数字,背面向上洗匀后随机抽取一张,将卡片上的数字记为a,然后放回,洗匀后再次随机取出一张,将卡片上的数字记为b,然后在平面直角坐标系中画出点M(a,b)的位置.
(1)请用树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园安全受到全社会的广泛关注,某市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
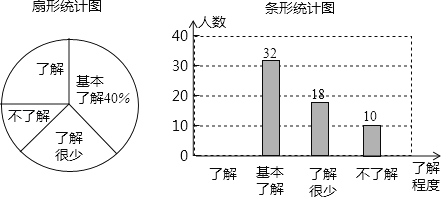
(1)在这次活动中抽查了多少名中学生?
(2)若该中学共有学生1600人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”程度的人数.
(3)若从对校园安全知识达到“了解程度的2个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m).
参考值:sin37°=0.60,cos37°=0.80,tan37°=0.75.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com