
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
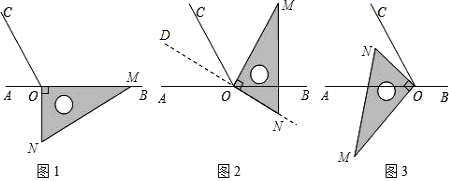
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
【答案】(1)ON平分∠AOC,理由见解析;(2)10或40;(3)30°.
【解析】
试题分析:(1)由角的平分线的定义和等角的余角相等求解;
(2)由∠BOC=120°可得∠AOC=60°,则∠RON=30°,即旋转60°或240°时ON平分∠AOC,据此求解;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,然后作差即可.
解:(1)直线ON平分∠AOC.理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON(对顶角相等),
∴∠COD=∠AOD,
∴OD平分∠AOC,
即直线ON平分∠AOC.
(2)∵∠BOC=120°
∴∠AOC=60°,
∴∠BON=∠COD=30°,
即旋转60°时ON平分∠AOC,
由题意得,6t=60°或240°,
∴t=10或40;
(3)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.


科目:初中数学 来源: 题型:
【题目】如图两个同心圆,大圆的半径为5,小圆的半径为1,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( )
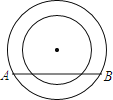
A.8≤AB≤10 B.8<AB≤10 C.4≤AB≤5 D.4<AB≤5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
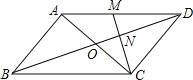
(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)已知:a=﹣5,b=2时,求代数式a2﹣3b的值.
(2)当a=﹣1,b=﹣3时,求代数式a2+2ab+b2的值
(3)已知:有理数m在原点右侧并且和原点距离4个单位,a,b互为相反数,且都不为零,c,d互为倒数.求:2(a+b)﹣(![]() ﹣3cd)﹣m的值.
﹣3cd)﹣m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com