
【题目】解方程
(1)3x+7=32﹣2x
(2)8x=﹣2(x+4)
(3)![]() ﹣
﹣![]() =1
=1
(4)3﹣![]() =3x﹣1.
=3x﹣1.
【答案】(1)x=5;(2)x=﹣0.8;(3)x=6;(4)x=![]() .
.
【解析】
试题分析:(1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解:(1)移项合并得:5x=25,
解得:x=5;
(2)去括号得:8x=﹣2x﹣8,
移项合并得10x=﹣8,
解得:x=﹣0.8;
(3)去分母得:3(x+2)﹣2(x+3)=6,
去括号得:3x+6﹣2x﹣6=6,
移项合并得:x=6;
(4)去分母得:6﹣x+1=6x﹣2,
移项合并得:7x=8,
解得:x=![]() .
.


科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍。乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠。该班需球拍5副,乒乓球若干盒(不小于5盒)。
问:(1)设购买乒乓球x盒时,在甲家购买所需多少元?在乙家购买所需多少元?(用含x的代数式表示,并化简)(4分)
(2)当购买乒乓球多少盒时,两种优惠办法付款一样?(2分)
(3)当购买30盒乒乓球时,若让你选择一家商店去办这件事,你打算去哪家商店购买?为什么?(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知大长方形ACFH的面积为572,被分割成六个小正方形,设最小的正方形边长a,第二小的正方形边长为b.
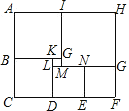
(1)a与b的关系为 ;
(2)求a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1,2,3,4,5组.

(1)求抽取了多少名男生测量身高?
(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm及170cm以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个布袋中装有2个红球和2个篮球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,不放回继续再摸第二个球,求两次都摸到红球的概率;
(2)在这4个球中加入x个用一颜色的红球或篮球后,进行如下试验,搅匀后随机摸出1个球记下颜色,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到红球的概率稳定在0.80,请推算加入的是哪种颜色的球以及x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
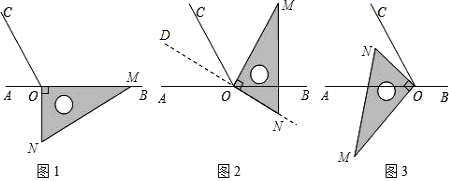
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
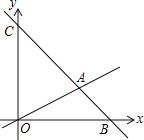
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com