
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
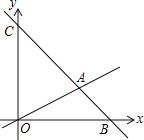
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.
【答案】(1)y=﹣x+6;(2)12;(3)M1(1,![]() )或M2(1,5).
)或M2(1,5).
【解析】
试题分析:(1)利用待定系数法即可求得函数的解析式;
(2)求得C的坐标,即OC的长,利用三角形的面积公式即可求解;
(3)当△OMC的面积是△OAC的面积的![]() 时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
解:(1)设直线AB的解析式是y=kx+b,
根据题意得:![]() ,
,
解得:![]() ,
,
则直线的解析式是:y=﹣x+6;
(2)在y=﹣x+6中,令x=0,解得:y=6,
S△OAC=![]() ×6×4=12;
×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=![]() ,
,
则直线的解析式是:y=![]() x,
x,
∵当△OMC的面积是△OAC的面积的![]() 时,
时,
∴M的横坐标是![]() ×4=1,
×4=1,
在y=![]() x中,当x=1时,y=
x中,当x=1时,y=![]() ,则M的坐标是(1,
,则M的坐标是(1,![]() );
);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,![]() )或M2(1,5).
)或M2(1,5).


科目:初中数学 来源: 题型:
【题目】化简下列各式
(1)a+[2a﹣2﹣(4﹣2a)]
(2)![]() x﹣(2x﹣
x﹣(2x﹣![]() y2)+(﹣
y2)+(﹣![]() )
)
(3)3x2+[2x﹣(﹣5x2+4x)+2]﹣1
(4)![]() (﹣3ax2﹣ax+3)﹣(﹣ax2﹣
(﹣3ax2﹣ax+3)﹣(﹣ax2﹣![]() ax﹣1)
ax﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,直线a,b被直线c所截,且∠1+∠2=180°.求证:a∥b.
(2)如图2,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
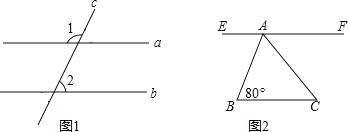
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)已知:a=﹣5,b=2时,求代数式a2﹣3b的值.
(2)当a=﹣1,b=﹣3时,求代数式a2+2ab+b2的值
(3)已知:有理数m在原点右侧并且和原点距离4个单位,a,b互为相反数,且都不为零,c,d互为倒数.求:2(a+b)﹣(![]() ﹣3cd)﹣m的值.
﹣3cd)﹣m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com