练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】三个互不相等的有理数，既可表示为1，a+b，a的形式，又可表示为0，，b，的形式，则a1992+b1993= ．

    【答案】2

    【解析】

    试题分析：根据三个有理数互不相等，又可以用两种方法表示，也就是这两组数分别对应相等，利用互斥原理，即可推理出a、b的值．

    解：由于三个互不相等的有理数，既可表示为1，a+b，a的形式，又可表示为0，，b的形式，也就是说这两个三数组分别对应相等，于是可以断定，a+b与a中有一个为0，与b中有一个为1，但若a=0，会使没意义，所以a≠0，只能是a+b=0，即a=﹣b，又a≠0，则=﹣1，由于0，，b为两两不相等的有理数，在=﹣1的情况下，只能是b=1．于是a=﹣1．

    所以，a1992+b1993=（﹣1）1992+（1）1993=1+1=2．

    故答案为：2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

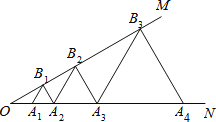
    【题目】如图，已知∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA2=4，则△AnBnAn+1的边长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法不正确的是（ ）

    A. 三角形的一个外角等于两个内角的和 B. 三角形具有稳定性

    C. 四边形的内角和与外角和相等 D. 角是轴对称图形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

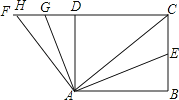
    【题目】如图，在矩形ABCD中，AC是对角线，点E是BC的中点，连接AE，AB=4，BC=3，将∠BAE绕点A逆时针旋转，使∠BAE的两边分别与线段CD的延长线相交于点G，H．当AH=AC时，CG= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若线段AB=10cm，C是线段AB上的任意一点，M、N分别是AC和CB的中点，则MN= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程

    （1）3x+7=32﹣2x

    （2）8x=﹣2（x+4）

    （3）﹣=1

    （4）3﹣=3x﹣1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a＞0）与x轴交于点O、M．对称轴为直线x=2，以OM为直径作圆A，以OM的长为边长作菱形ABCD，且点B、C在第四象限，点C在抛物线对称轴上，点D在y轴负半轴上；

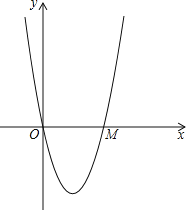
    （1）求证：4a+b=0；

    （2）若圆A与线段AB的交点为E，试判断直线DE与圆A的位置关系，并说明你的理由；

    （3）若抛物线顶点P在菱形ABCD的内部且∠OPM为锐角时，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果a、b、c是△ABC的三边，满足（b﹣3）2+|c﹣4|=0，a为奇数，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】化简下列各式

    （1）a+[2a﹣2﹣（4﹣2a）]

    （2）x﹣（2x﹣y2）+（﹣）

    （3）3x2+[2x﹣（﹣5x2+4x）+2]﹣1

    （4）（﹣3ax2﹣ax+3）﹣（﹣ax2﹣ax﹣1）

    查看答案和解析>>

    同步练习册答案