
【题目】在△ABC中,AB=AC,D、E分别在BC和AC上,AD与BE相交于点F.
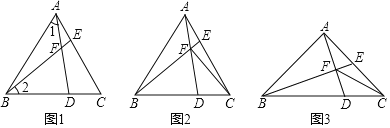
(1)如图1,若∠BAC=60°,BD=CE,求证:∠1=∠2;
(2)如图2,在(1)的条件下,连接CF,若CF⊥BF,求证:BF=2AF;
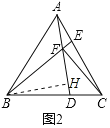
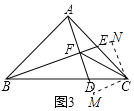
(3)如图3,∠BAC=∠BFD=2∠CFD=90°,若S△ABC=2,求S△CDF的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据等边三角形的判定定理得到△ABC为等边三角形,得到AB=BC,∠ABC=∠C=60°,证明△ABD≌△BCE,根据全等三角形的性质证明结论;
(2)过B作BH⊥AD,根据全等三角形的性质得到∠BAD=∠CBE,证明△AHB≌△BFC,根据全等三角形的性质解答;
(3)过C作CM⊥AD交AD延长线于M,过C作CN⊥BE交BE延长线于N,根据角平分线的性质得到CM=CN,证明△AFB≌△CMA,根据全等三角形的性质得到BF=AM,AF=CM,根据三角形的面积公式列式计算即可.
(1)证明:∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∴AB=BC,∠ABC=∠C=60°,
在△ABD和△BCE中,
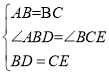 ,
,
∴△ABD≌△BCE(SAS),
∴∠1=∠2;
(2)如图2,过B作BH⊥AD,垂足为H,
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∵∠ABF+∠CBE=60°,
∴∠BFD=∠ABF+∠BAD=60°,
∴∠FBH=30°,
∴BF=2FH,
在△AHB和△BFC中,
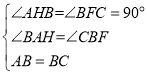
∴△AHB≌△BFC(AAS),
∴BF=AH=AF+FH=2FH,
∴AF=FH,
∴BF=2AF;
(3)如图3,过C作CM⊥AD交AD延长线于M,过C作CN⊥BE交BE延长线于N,
∵∠BFD=2∠CFD=90°,
∴∠EFC=∠DFC=45°,
∴CF是∠MFN的角平分线,
∴CM=CN,
∵∠BAC=∠BFD=90°,
∴∠ABF=∠CAD,
在△AFB和△CMA中,

∴△AFB≌△CMA(AAS)
∴BF=AM,AF=CM,
∴AF=CN,
∵∠FMC=90°,∠CFM=45°,
∴△FMC为等腰直角三角形,
∴FM=CM,
∴BF=AM=AF+FM=2CM,
∵![]()
∴S△BDF=2S△CDF,
∵AF=CM,FM=CM,
∴AF=FM,
∴F是AM的中点,
∴![]() ,
,
∵AF⊥BF,CN⊥BF,AF=CN,
∴S△AFB=S△BFC,
设S△CDF=x,则S△BDF=2x,
∴S△AFB=S△BFC=3x
∴![]() ,
,
则3x+3x+![]() x=2,
x=2,
解得,x=![]() ,即S△CDF=
,即S△CDF=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
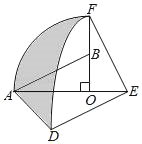
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分別以O、E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为![]() 米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
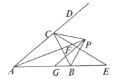
【题目】如图所示,在![]() 中,内角
中,内角![]() 与外角
与外角![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() ,
,![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() 、
、![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() 垂直平分
垂直平分![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )
A. ①②④B. ①③④C. ②③④D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( )

A. 30°B. 45°C. 60°D. 15°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com