【题目】以下说法正确的有（ ）
①正八边形的每个内角都是135°
②
与
是同类二次根式
③长度等于半径的弦所对的圆周角为30°
④反比例函数y＝﹣
，当x＜0时，y随x的增大而增大．
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①由正多边形的性质，即可求得正八边形的每个内角的度数；
②首先化简，则可求得
与
是同类二次根式；
③可求得长度等于半径的弦所对的圆周角为30°或150°；
④由反比例函数的性质，可得反比例函数y＝﹣
，当x＜0时，y随x的增大而增大．
解：①正八边形的每个内角都是：
＝135°，故①正确；
②∵
，
，
∴与是同类二次根式；故②正确；
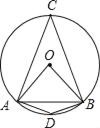
③如图：∵OA＝OB＝AB，
∴∠AOB＝60°，
∴∠C＝
∠AOB＝30°，
∴∠D＝180°﹣∠C＝150°，
∴长度等于半径的弦所对的圆周角为：30°或150°；故③错误；
④反比例函数y＝﹣，当x＜0时，y随x的增大而增大．故④正确．
故正确的有①②④，共3个．
故选C．
科目：初中数学 来源： 题型：
【题目】如图，在⊙O中，直径AB＝8，∠A＝30°，AC＝8
，AC与⊙O交于点D．
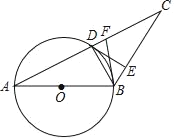
（1）求证：直线BD是线段AC的垂直平分线；
（2）若过点D作DE⊥BC，垂足为E，求证：DE是⊙O的切线；
（3）若点F是AC的三等分点，求BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“十字相乘法”能把二次三项式分解因式，对于形如ax2+bxy+cy2的x，y二次三项式来说，方法的关键是把x2项系数a分解成两个因数a1，a2的积，即a＝a1a2，把y2项系数c分解成两个因数，c1，c2的积，即c＝c1c2，并使a1c2+a2c1正好等于xy项的系数b，那么可以直接写成结果：ax2+bxy+cy2＝（a1x+c1y）（a2x+c2y）
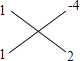
例：分解因式：x2﹣2xy﹣8y2
解：如右图，其中1＝1×1，﹣8＝（﹣4）×2，而﹣2＝1×（﹣4）+1×2∴x2﹣2xy﹣8y2＝（x﹣4y）（x+2y），而对于形如ax2+bxy+cy2+dx+ey+f的x，y的二元二次式也可以用十字相乘法来分解，
如图1，将a分解成mn乘积作为一列，c分解成pq乘积作为第二列，f分解成jk乘积作为第三列，如果mq+np＝b，pk+qj＝e，mk+nj＝d，即第1，2列、第2，3列和第1，3列都满足十字相乘规则，则原式＝（mx+py+j）（nx+qy+k）；
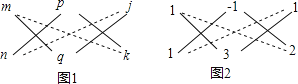
例：分解因式：x2+2xy﹣3y2+3x+y+2
解：如图2，其中1＝1×1，﹣3＝（﹣1）×3，2＝1×2；
而2＝1×3+1×（﹣1），1＝（﹣1）×2+3×1，3＝1×2+1×1；∴x2+2xy﹣3y2+3x+y+2＝（x﹣y+1）（x+3y+2）
请同学们通过阅读上述材料，完成下列问题：
（1）分解因式：6x2﹣7xy+2y2＝ x2﹣6xy+8y2﹣5x+14y+6＝
（2）若关于x，y的二元二次式x2+7xy﹣18y2﹣5x+my﹣24可以分解成两个一次因式的积，求m的值．
（3）已知x，y为整数，且满足x2+3xy+2y2+2x+4y＝﹣1，求x，y．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠ACB=90°，BE平分∠ABC，D是边AB上一点，以BD为直径的⊙O经过点E，且交BC于点F．
（1）求证：AC是⊙O的切线；
（2）若BF=6，⊙O的半径为5，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商城销售A，B两种自行车．A型自行车售价为2 100元/辆，B型自行车售价为1 750元/辆，每辆A型自行车的进价比每辆B型自行车的进价多400元，商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等．
（1）求每辆A，B两种自行车的进价分别是多少？
（2）现在商城准备一次购进这两种自行车共100辆，设购进A型自行车m辆，这100辆自行车的销售总利润为y元，要求购进B型自行车数量不超过A型自行车数量的2倍，总利润不低于13 000元，求获利最大的方案以及最大利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
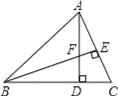
【题目】如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．
（1）求证：△ACD∽△BFD；
（2）当tan∠ABD=1，AC=3时，求BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数
的图象与
轴正半轴相交于
、
两点，与
轴相交于点
，对称轴为直线
，且
，则下列结论：
①
；②
；③
；④关于的方程
有一个根为
，其中正确的结论个数有（ ）
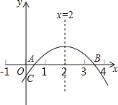
A. 
个 B. 
个 C. 
个 D. 
个
查看答案和解析>>
科目：初中数学 来源： 题型：
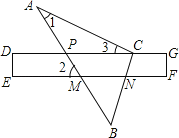
【题目】如图，将三角尺的直角顶点放在直尺的一边上，∠1＝30°，
（1）作出△APC的PC边上的高；
（2）若∠2＝51°，求∠3；
（3）若直尺上点P处刻度为2，点C处为8，点M处为3，点N处为7，求S△BMN：S△BPC的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
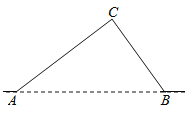
【题目】如图，从
地到
地的公路需经过
地，图中
，
，
，因城市规划的需要，将在
两地之间修建一条笔直的公路.
（Ⅰ）求改直的公路
的长；
（Ⅱ）问公路改直后比原来缩短了多少
？（参考数据：
，
，
，
取
.）（结果保留小数点后一位）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com